
- DP를 설명하기에 앞서 planning과 learning의 차이를 먼저 봅시다.
-> Planning : environment의 model을 알고서 문제를 푸는 것.
-> Learning : environment의 model을 모르지만 상호작용을 통해서 푸는 것.
=> DP는 planning으로서 environment의 model에 대해 안다는 전제로 Bellman equation을 사용해서 문제를 푸는 것을 말한다.
=> 강화학습은 learning이지만 DP에 기반을 두고 발전했다.
1. Policy Iteration
- DP는 prediction과 control 두 step으로 나뉜다.
-> 현재의 policy에 대하여 value function을 구하고 (prediction) value function을 토대로 더 나은 policy를 구한다.
=> 이와 같은 과정을 반복한다. (iteration)

- Policy evaluation은 prediction 문제를 푸는 것이다.
-> 현재 주어진 policy에 대한 true value function을 Bellman equation을 통해서 푼다.
=> 현재 policy를 가지고 true value function을 구하는 것을 one step backup이라고 한다.
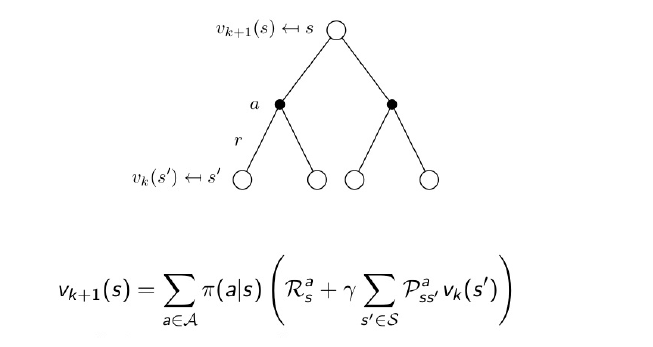
-> 앞선 게시물의 Bellman equation의 그림과 다른 것을 iteration number \( k \)가 붙은 것이다.
-> 현재 state의 value function을 update하기 위해서 현재 state에서 특정 action을 선택했을 때의 reward와 그 action에서 state transition probability matrix를 고려하여 얻어진 value function의 총합을 사용한다.
=> 즉, 현재 state의 다음 state에 대한 정보들을 사용한다.
=> 중요한 점은, 모든 state에 대해서 동시에 한번씩 Bellman equation을 계산해서 update한다.
=> 차례 차례 state 별로 구하는 것이 아니고 한번에 계산해서 한번에 value function을 update한다.
1) Policy evaluation
- grid world의 example을 보자.

-> action은 상/ 하/ 좌/ 우 네 방향으로 구분되고, time step이 지날 때 마다 -1의 reward가 쌓인다.
-> 각 방향 (action)을 선택할 때의 policy는 0.25로 동일하다.
=> terminal state로 가장 빨리 도달할 수 있는 방법을 찾는 policy를 구하는 것이 DP이다.
-> DP는 evaluation과 improve 두 단계로 나누어진다.
=> Evaluation은 현재의 policy가 얼마나 좋은가를 판단하는 것이다.
=> 판단 기준은 해당 policy를 따라갈 경우 받게 될 value function이다.
- 처음 policy는 모든 state에서 똑같은 확률로 상/ 하/ 좌/ 우로 움직이는 것이다.

-> k = 1 일 때 모든 state의 value function V는 V = (상 + 하 + 좌 + 우) = -1 * 0.25 + -1 * 0.25 + -1 * 0.25 + -1 * 0.25 = -4 로 동일하다.
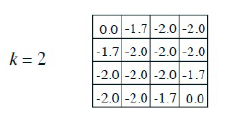
-> k = 2 일 때 (2, 2)에 있는 (왼쪽 제일 위를 원점이라고 할 때) state의 value function을 보자.
=> V (k (2,2) = 2) = 총합 (각 action에 대해서) {(이전 step의 V * discounting factor) + (다음 action을 선택했을 때 얻는 value function * policy)} ==> 나중에 수식으로 정리
= 총합 (각 action에 대하여) {0.25 * (-1 (현재 action으로써 얻게되는 reward) + -1 (이전 step에서의 value function * discounting factor))} = sigma(action{상, 하, 좌, 우}) (0.25 * (-1 + -1)) = -2
-> k = 2 일 때 (2,1)에 있는 state의 value function은 다음과 같다.
=> V (k (2,1) = 2) = 상 (튕겨서 되돌아 온다): 0.25 * (-1 + -1) + 하: 0.25 * (-1 + -1) + 좌: 0.25 * (-1 + 0) + 우: 0.25 * (-1 + -1) = -1.7

-> discounting factor 뒤의 state transition matrix를 고려한 value function 값의 총합은 현재에선 그냥 그 상태의 value function이라고 하자. (이 문제에선 정의되어 있지 않으니까 state transition matrix = 1)

-> k = 3 : V = 0.25 * (-1 + -1.7) + 0.25 * (-1 + -2.0) + 0.25 * (-1 + 0) + 0.25 * (-1 + -2.0) = -2.425 = -2.4
=> 현재 state의 value는 (transition 할 때의 reward)와 (state transition matrix와 이전 value를 곱한 값)의 합에 policy를 곱한 것과 같다.
=> 천천히 읽고 이해하자.
=> 이런 식으로 무한대까지 계산을 이어가면 현재 random policy에 대한 true value function을 구할 수 잇다.
=> 이런 과정을 policy evaluation이라고 한다.
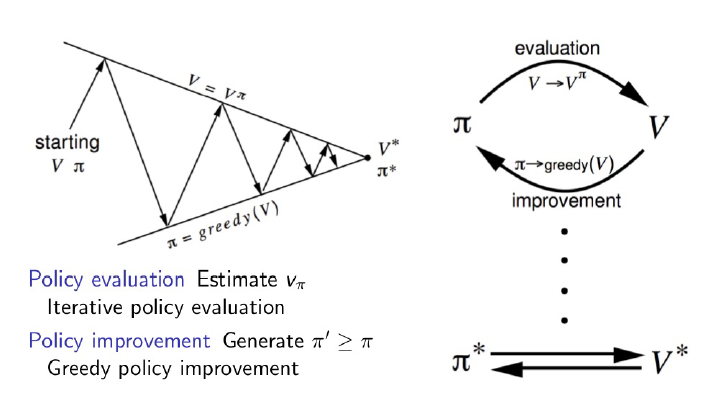
2) Policy iteration
: Random policy에 대한 true value function을 얻은 이후 policy를 더 나은 policy로 update 해줘야 한다.
-> 해당 과정을 통해 optimal policy로 가까워질 수 있고, 이런 과정을 policy iteration이라고 한다.
- Greedy improvement
: 다음 state 중에서 가장 높은 value function을 가진 state로 가는 방법.
-> max를 취하는 것과 같다.

- 위에서 구한 value function을 토대로 improve 과정을 한번 진행하면 다음과 같은 결과가 나온다.
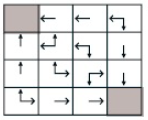
-> 위의 grid world는 매우 작은 경우의 수를 가정하고 있기 때문에 improve 결과를 위의 그림과 같이 쉽게 구할 수 있지만, 일반적으론 evaluation과 improve를 계속 반복해야 optimal policy를 구할 수 있다.
=> 이러한 과정을 policy iteration이라고 한다.
2. Value Iteration
: Policy iteration과 다른 점은 Bellman Expectation Equation이 아닌 Bellman Optimality Equation을 사용하는 것이다.

- Bellman Optimality Equation은 optimal value function들 사이의 관계식이다.
-> Policy iteration은 evaluation 할 때 모든 action을 고려하여 (grid world 에서의 동/ 서/ 남 북) value function을 update 해줘야하는 단점이 있는데 이 과정을 하나의 state에 대해서만 evaluation하는 것이 value iteration이다.
=> 현재 value function을 계산하고 update할 때 max를 취함으로써 greedy하게 improve하는 효과를 준다.
=> evaluation 한번 + improvement = value iteration
- Terminal state가 하나인 grid world 예제를 보자.
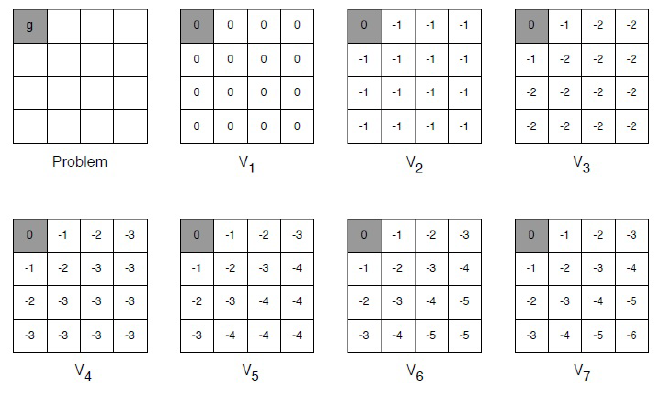
-> 아주 간단하게 agent가 특정 위치에 있을 때 terminal state가 아니면 time step 마다 -1의 reward를 받는 상황이라고 가정해보자.
-> Value iteration에서의 update 과정은 매우매우 단순하다.
=> 다음 value function = max(reward + 이전 value function (옮겨갈 자리의 value function)) 이다.
=> 즉, terminal state를 원점으로 할 때 (2, 0)에 있는 state의 value function은
V2 = -1 (reward) + 0 (모든 방향 동일) = -1
V3 = -1 (reward) + -1 (서쪽 방향) = -2
3. Sample Backup

- DP는 MDP에 대한 정보를 다 가지고 있을 때 optimal policy를 구할 수 있다.
- DP는 full-width backup (한번 update할 때 모든 가능한 successor state의 value function을 통해 update하는 방법) 을 사용학 때문에 한번의 backup에도 많은 계산을 사용해야한다.
-> 따라서 위와 같이 작은 grid world는 괜찮지만 state 숫자가 늘어날수록 계산량이 많아져 MDP가 크거나 잘 알지 못할 때 DP를 적용시킬 수 없다.
- Sample back-up
: 위에서 서술한 문제점을 해결하기 위한 방법
- 모든 가능한 successor state와 action을 고려하는 것이 아닌 sampling을 통해서 하나의 길만 가보고 그 정보를 토대로 value function을 update한다.
-> 계산의 효율을 증가시키고 model-free가 가능하다.
=> Sample backup은 <S, A, R, S'>을 training set으로 하여 실제로 나온 reward와 sample transition으로 문제를 해결할 수 있다. (reward function과 transition dynamics를 대체한다.)
=> MPD model을 몰라도 optimal policy를 구할 수 있게 되고, learning이 되는 것이다.
=> 즉, DP를 sampling을 통해서 풀면 Reinforcement learning이 시작된다.

-> 이것은 다음 장의 monte-carlo에서 자세히 설명할 것이다.
출 처 : Fundamental of Reinforcement Learning
저 자 : Woong won, Lee
'Study > Reinforcement learning' 카테고리의 다른 글
| 강화학습_(7) - Markov Decision Process (MDP) (0) | 2019.11.07 |
|---|---|
| 강화학습_(6) - Neural Network의 학습 방법 - Gradient descent, Back-propagation (0) | 2019.10.30 |
| 강화학습_(5) - 머신 러닝 분류 - 지도 학습, 비지도 학습, 강화 학습 (0) | 2019.10.30 |
| 강화학습_(4) - Math Preliminary_2 (0) | 2019.10.23 |
| 강화학습_(4) - Math Preliminary_1 (0) | 2019.10.22 |