References : 조행래 교수님 (영남대학교), 박종혁 교수님 (서울과학기술대학교)의 강의 / 강의자료에 기반한 내용입니다. + 제가 공부한 내용
1. 순서 리스트 (Ordered list)란?
- 정의 : 데이터들의 순서가 유지되는 집합
EX)
-> (일 월 화 수 목 금 토)
-> (A, 2, 3, 4, 5, 6, 7, 8. 9, 10, J, Q, K)
-> (지하실, 로비, 일층, 이층)
- 순서 리스트에 적용 가능한 연산들
순서가 정해져 있기 때문에 다음과 같은 연산이 가능합니다.
-> 리스트의 길이 n의 계산
-> 리스트의 모든 데이터들을 왼쪽에서 오른쪽으로 읽기
-> 리스트로부터 i 번째 데이터를 검색, 0≤i<n
-> 리스트로부터 i 번째 데이터를 대체, 0≤i<n
-> 리스트의 i 번째 위치에 새로운 데이터를 추가
=> 그 결과로 기존의 i 부터 n–1 까지의 데이터들이 i+1 부터n 까지 한 칸씩 뒤로 이동
-> 리스트의 i 번째 데이터를 삭제
=> 그 결과로 기존의 i+1 부터 n–1 까지의 데이터들이 i 부터 n–2 까지 한 칸씩 앞으로 이동
2. 다항식
순서 리스트를 사용해 다항식을 구현할 수 있습니다.
- 순서 리스트를 구현하는 2 가지 방법 : 배열, 연결 리스트
(연결 리스트는 해당 게시물 이후에 큐와 스택에 대해 배우고, 그 다음 게시물에서 설명 드릴 개념입니다.)
- 다항식이란?

추상 데이터 타입 (= Abstract Data Type : ADT)

다항식을 ADT를 사용하여 표현하면 위와 같습니다.
각 함수명에 대하여 자세한 사항을 제외하고 간단히 기능만 명세한 것입니다.
이전 게시물에서 확인했습니다.
이제 이와 같은 다항식을 C 언어에서 구현해보겠습니다.
3. 다항식 저장
1) 모든 지수의 계수들을 내림차순으로 저장
EX)
#define MAX_DEGREE 101
typedef struct{
int degree;
float coef[MAX_DEGREE];
} polynomial;
EX)
p(x) = 2*x^3 + 1*x^2 + 1
=> [최고차항의 차수, (계수 내림차순 정리)]
=> [3, (2, 1, 0, 1)]
이런 방법은 다음과 같은 경우에 메모리 손실이 아주 큽니다.
EX)
p(x) = 100*x^100 + 1
=> [최고차항의 차수, (계수 내림차순 정리)]
=> [100, (100, 0, 0, 0, ..., 1)]
따라서 다으모가 같은 방법이 제시 될 수 있습니다.
2) 지수와 계수를 모두 저장
- 각 다항식을 (start, end)의 쌍으로 표현합니다.
- 모든 다항식을 저장하기 위한 전역변수 terms[]를 사용합니다.
EX)
#define MAX_TERMS 100
typedef struct {
float coef;
int expon;
} polynominal;
polynominal terms[MAX_TERMS]; // 구조체의 배열입니다.
// terms[i].coef 와 같이 사용할 수 있습니다. (곧 설명할거에요!)
int avail = 0;
EX)
p(x) = 100*x^100 + 1
=> [(계수, 지수), ..., (계수 지수)]
=> [(100, 100), (1, 0)]
근데 이것도 문제가 있습니다.
다항식의 모든 항들의 계수가 0이 아닌 경우 이전 보다 많은 수의 메모리가 필요합니다.
목적에 맞게 다항식을 배열에 저장하는 것이 중요한 것 같습니다.
4. 다항식 구현
다항식을 구현하기 위해서 3-2)에서 다뤘던 항의 계수와 지수를 모두 저장하는 방법을 사용하겠습니다.
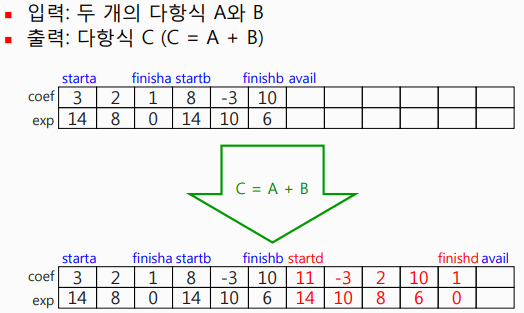
다항식 A의 시작인 가장 큰 차수의 항은 starta로 저장됩니다.
가장 작은 차수는 finisha로 저장됩니다.
다항식 B의 시작인 가장 큰 차수의 항은 startb로 저장됩니다.
가장 작은 차수는 finishb로 저장됩니다.
두 다항식은 연결되어 저장되고, 배열의 끝 부분은 avail을 통해 다항식의 저장이 끝났다는 것을 알려줍니다.
바로 구현해보면서 확인하겠습니다.
좀 지루할 수 있는데 필요한 과정이니까 코드를 잘 봐주시길 바랍니다.
설명은 코드 출력 결과 이후에 하겠습니다.
코드를 한번 쭉 보면서 한숨 두번 정도 쉬고, 설명 보고, 다시 코드를 보면 이해와 기억이 더 잘 될 겁니다.
알고리즘은 아래의 이미지를 구현한 것입니다.

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX_TERMS 100
#define COMPARE(x, y) (((x)<(y)) ? -1 : ((x)==(y)) ? 0 : 1)
typedef struct {
float coef;
int expon;
} polynominal;
polynominal terms[MAX_TERMS];
polynominal AAA;
int avail = 0;
void attach(float coefficient, int exponent) {
if (avail >= MAX_TERMS) {
fprintf(stderr, "Too many terms in the polynomial \n.");
exit(1);
}
terms[avail].coef = coefficient;
terms[avail].expon = exponent;
printf("%d = 계수 : %f, 지수 : %d\n", avail, terms[avail].coef, terms[avail].expon);
avail++;
}
void padd(int starta, int finisha, int startb, int finishb, int *startd, int *finishd) {
// d = a + b
float coefficient;
printf("Start\n");
*startd = avail;
while (starta <= finisha && startb <= finishb) {
printf("--------------------------------------------\n");
printf("starta = %d, finisha = %d\n", starta, finisha);
printf("startb = %d, finishb = %d\n", startb, finishb);
switch (COMPARE(terms[starta].expon, terms[startb].expon)) {
case -1: // a.expon < b.expon
printf("b++?\n");
attach(terms[startb].coef, terms[startb].expon);
startb++;
break;
case 0: // equal exponents
coefficient = terms[starta].coef + terms[startb].coef;
printf("a&b++?\n");
if (coefficient)
attach(coefficient, terms[starta].expon);
starta++;
startb++;
break;
case 1: // a.expon > b.expon
printf("a++?\n");
attach(terms[starta].coef, terms[starta].expon);
starta++;
break;
}
}
printf("--------------------------------------------\n");
printf("Finish\n");
printf("--------------------------------------------\n");
printf("starta = %d, finisha = %d\n", starta, finisha);
printf("startb = %d, finishb = %d\n", startb, finishb);
for (; starta <= finisha; starta++){
attach(terms[starta].coef, terms[starta].expon);
}
for (; startb <= finishb; startb++){
attach(terms[startb].coef, terms[startb].expon);
}
*finishd = avail-1;
printf("--------------------------------------------\n");
printf("startd = %d, finishd = %d\n", *startd, *finishd);
}
int main(void) {
int startd, finishd;
/*-------------------------------*/
terms[0].coef = 3;
terms[0].expon = 14;
terms[1].coef = 2;
terms[1].expon = 8;
terms[2].coef = 1;
terms[2].expon = 0;
/*-------------------------------*/
terms[3].coef = 8;
terms[3].expon = 14;
terms[4].coef = -3;
terms[4].expon = 10;
terms[5].coef = 10;
terms[5].expon = 6;
/*-------------------------------*/
avail = 6;
// padd(int starta, int finisha, int startb, int finishb, int *startd, int *finishd)
padd(0, 2, 3, 5, &startd, &finishd);
printf("Addition was finished just before.\n");
for (int i = startd; i <= finishd; i++){
printf("terms[%2d].coef = %5.2f, terms[%2d].expon = %2d\n", i, terms[i].coef, i, terms[i].expon);
}
return 0;
}
코드 실행 결과는 다음과 같습니다.

이 코드는 조행래 교수님의 KMOOC 강의 자료에 있는 코드를 구현한겁니다.
강의 자료에는 padd와 attach 부분만 나와있습니다.
하... 진짜 힘들었어요... 이왕 올려주실거면 다 올려주시지 ㅜㅜ
괄호랑 함수 몇 줄이 빠져있고, main 부분이 없어서 수정하기 참 힘들었습니다...
전반적으로 이해하기 어려운 알고리즘은 아닙니다.
1) terms[i]에 다항식 a와 다항식 b의 항을 차례대로 계수/지수를 나눠서 저장해줍니다.
이때 항이 하나 지날 때 마다 i를 하나 증가시켜줍니다.
2) starta와 finisha는 다항식 a를 저장한 배열 인덱스의 시작과 끝입니다. (b도 같습니다.)
avail은 항을 전부 저장하고 비어있는 부분을 가리키는 지표입니다.
3) term[avail] 부터 두 다항식을 더한 항의 계수(.coef)와 지수(.expon)가 저장됩니다.
저장되는 항은 다음과 같습니다.
- a의 지수가 더 클 때? (-1)
1]
terms[avail].coef = terms[starta].coef
terms[avail].expon = terms[starta].expon
// 두 다항식의 가장 큰 항 중 더 큰 항의 계수와 지수가 먼저 저장됩니다.
2]
avail = avail + 1
// avail은 다음 칸으로 넘어갑니다. (방금 담은 항보다 작은 차수의 항을 저장하기 위해서)
- a와 b의 지수가 같을 때? (0)
1]
terms[avail].coef = terms[starta].coef + terms[startb].coef
terms[avail].expon = terms[starta].expon
// 두 다항식의 항의 차수가 동일하기 때문에 항의 지수 부분 (expon)은 둘 중에 아무거나 (여기선 다항식 a의 지수) 저장하고, 계수는 두 항의 계수를 더해줍니다.
2]
avail = avail + 1
// avail은 다음 칸으로 넘어갑니다. (방금 담은 항보다 작은 차수의 항을 저장하기 위해서)
- b의 지수가 더 클 때? (1)
1]
terms[avail].coef = terms[startb].coef
terms[avail].expon = terms[startb].expon
// 두 다항식의 가장 큰 항 중 더 큰 항의 계수와 지수가 먼저 저장됩니다.
2]
avail = avail + 1
// avail은 다음 칸으로 넘어갑니다. (방금 담은 항보다 작은 차수의 항을 저장하기 위해서)
4) startd와 finishd는 더한 결과값의 배열 인덱스 시작과 끝입니다.
코드 시작 전에 보여드렸던 그림과 알고리즘을 비교해가며 이해하시면 금방 이해 할 수 있습니다.
다음 게시물에선 드디어 스택과 큐에 대해서 설명드리겠습니다.
'Programming > C' 카테고리의 다른 글
| [자료구조 C 언어] C 프로그래밍 자료구조 - 4 : 배열을 사용한 스택 (Stack) (0) | 2020.03.04 |
|---|---|
| [자료구조 C 언어] C 프로그래밍 자료구조 - 3 (추가) : 희소 행렬 (1) | 2020.02.27 |
| [자료구조 C 언어] C 프로그래밍 자료구조 - 2 : 배열과 구조체 (0) | 2020.02.27 |
| [자료구조 C 언어] C 프로그래밍 자료구조 - 1 : 자료구조와 알고리즘의 개념, 알고리즘 복잡도 (시간 복잡도) (0) | 2020.02.26 |
| [자료구조 C 언어] C 프로그래밍 기초 - 7 : 이중 포인터와 2차원 배열의 관계 (4) | 2020.02.25 |