단순한 정리와 활용을 원하시는 분은 마지막 코드를 참조해주세요.
주석만으로도 충분히 이해하실 수 있습니다.
* 게시물 내의 모든 그림과 사진의 무단 도용을 금지합니다.
저번 게시물에서 그래프의 기본 개념에 대해 알아보았습니다.
이번에는 그래프를 사용한 기초 연산에 대해 공부해보겠습니다.
일단 기초적인 그래프 연산들은 다음과 같습니다.
1) 깊이우선 탐색 (Depth First Search)
2) 너비우선 탐색 (Breadth First Search)
3) 연결요소 (Connected Components)
4) 신장트리 (Sapnning Trees)
5) 단절점 (Articulation Points)
1. 깊이 우선 탐색 (Depth First Search)
DFS 알고리즘은 아래의 특징을 가지고 있습니다.
1) 출발 정점, v의 인접 리스트부터 방문
2) v에 인접하면서 아직 방문하지 않은 정점 w를 선택
3) w를 시작점으로 하여, 다시 깊이 우선 탐색 시작
4) 순환 알고리즘 (recursive algorithm == 재귀 함수)을 이용하여 구현

무조건 다음으로 가는 노드에서 방문하지 않은 인접 노드가 있을 시 인접 노드로 방문

2. 너비 우선 탐색 (Breadth First Search)
BFS 알고리즘은 아래의 특징을 가지고 있습니다.
1) 출발 정점 v의 인접 리스트부터 방문
2) v에 인접한 모든 vertex들을 먼저 방문
3) 그 다음 v에 인접한 첫번째 vertex에 인접한 vertex 중에서 아직 방문하지 않은 vertex들을 다시 차례대로 방문 (Queue를 이용)

하나 주변 싹 돌고, 첫번째 노드의 주변 싹 돌고 반복
기준 노드를 큐에 저장하고, 해당 노드의 인접노드를 싹 돈다 (돌면서 방문한 노드는 FALSE->TRUE)
돌면서 각 노드를 큐에 저장하고 (가장 먼저 빠져나올 애가 첫번째 방문된 노드)
다 돌면, 큐에 저장된 첫번째로 방문된 노드를 기준으로 다시 위의 과정을 반복한다.

3. 연결 요소 (Connected Component)
무방향성 그래프가 연결되어 있는지 검사할 때 DFS나 BFS 알고리즘을 사용합니다.
이때 방문하지 않은 정점이 존재하지 않을 때 해당 요소를 출력합니다.
출력된 요소가 있을 시 해당 그래프는 연결되어 있지 않습니다.
4. 신장 트리 (Spanning Tree)
신장트리란 그래프 G에 포함된 edge들로 구성되며, G의 모든 vertex들을 포함하는 트리입니다.
즉, vertex는 똑같고 G의 edge 집합에 포함된 edge로만 구성된 트리를 말합니다.
DFS나 BFS를 이용하여 신장 트리를 아래와 같이 구성할 수있습니다.

5. 단절점 (Articulation Points)
단절점이란 그래프 G의 특정 vertex에 연결된 edge들을 모두 삭제할 경우, G가 두 개 이상의 연결 요소들로 분할될 때
해당 vertex를 단절점이라고 합니다.
5-1. 이중 결합 그래프 (Biconnected graph)
단절점이 없는 connected graph를 말합니다.
5-2. 이중 결합 요소 (Biconnected component)
연결 그래프 G에서 maximal binonnected subgraph, H 입니다.
이때 maximal의 의미는 이중 연결 되어있으면서, H를 완전히 포함하는 부분 그래프가 G에 존재하지 않는 것을 말합니다.
조금 애매한데 다음 그림을 보며 한번 더 설명 드리겠습니다.
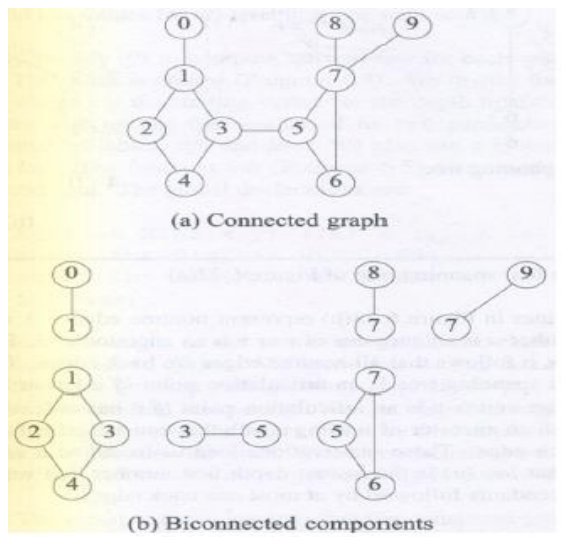

이중 결합 그래프는 그래프 내의 어떤 정점을 삭제 하더라도 그래프가 나뉘어지지 않는 그래프를 말합니다.
이중 결합 요소는 그래프 (이중 결합 그래프를 포함한 모든 그래프)에서 이중 결합 되어 있는 부분 그래프를 나열했을 때
다른 부분 그래프에 포함되지 않는 이중 결합 되어 있는 부분 그래프를 말합니다.
따라서 이중 결합 그래프에서 이중 결합 요소는 자기 자신 밖에 없습니다.
(모든 정점이 이중 결합 되어 있지만, 모두 다 이중 결합 그래프가 아우를 수 있기 때문입니다.)
그래프를 사용한 깊이우선 탐색과 너비우선 탐색 구현
* 그래프 BFS, DFS ADT
/*---------Graph ADT---------*/
Graph* Init_Graph(void); // 그래프 구성을 위한 구조체 포인터를 초기화 합니다.
void Add_Vertex(Graph* g); // 그래프에 정점을 추가합니다. 아직 연결은 안 된 상태입니다.
void Add_Edge(Graph* g, int u, int v); // 추가된 정점을 이어주는 간선을 생성합니다.
void Check_Link(Graph* g, int u, int v); // 두 정점이 간선으로 이어져 있는지 검사합니다.
void Delete_Vertex(Graph* g, int u); // 정점과 해당 정점에 연결된 모든 간선을 삭제합니다.
void Delete_Edge(Graph* g, int u, int v); // 두 정점 사이를 잇는 간선을 삭제합니다.
void DFS(Graph *g, int n); // 깊이 우선 탐색 알고리즘을 실행합니다.
void Depth_First_Search(Graph* g, int n); // 깊이 우선 탐색 알고리즘에 대한 코드가 저장되어 있습니다.
void BFS(Graph *g, int n); // 넓이 우선 탐색 알고리즘을 실행합니다.
void Breath_First_Search(Graph* g, int n); // 넓이 우선 탐색 알고리즘에 대한 코드가 저장되어 있습니다.
void Add_Queue(int n); // 넓이 우선 탐색을 위한 큐입니다.
int Delete_Queue(void); // 넓이 우선 탐색을 위한 큐입니다.
/*---------------------------*/
1. 그래프를 위한 구조체를 초기화 합니다.
그래에 추가된 정점의 갯수를 반환하는 구조체 멤버 변수인 n을 0으로, 연결된 정점에 대한 정보를 저장하는 adj_list에 NULL 값을 저장해줍니다.
adj_list에는 향후 Add 관련 함수에서 정점 정보 추가 시 정점을 저장할 수 있는 메모리가 동적할당 됩니다.
Graph* Init_Graph(void){
Graph* g = (Graph*)malloc(sizeof(Graph));
g->n = 0;
for(int i = 0; i < MAX_VERTEX; i++)
g->adj_list[i] = NULL;
return g;
}
2. 정점 추가, 간선 추가
Add_Vertext
그래프를 구성하려면 일단 정점이 있어야합니다.
따라서, 원하는 만큼 Add_Verte를 실행해주면 해당하는 adj_list가 생성되고
정점에 대한 정보를 저장할 수 있도록 List 구조체의 메모리가 할당됩니다.
Add_Edge
우선 정점을 생성한 뒤에 실행해야 합니다.
생성된 정점들을 이어주는 간선을 생성합니다.
예를들어 그래프에 정점 u와 v가 추가되었을 때, 둘을 잇는 간선을 생성하는 것을 확인해보겠습니다.
g->adj_list[u]는 v와 연결해주고, 반대의 경우도 동일합니다.
이때 그래프를 처리하는 편의성을 위해 다음과 같은 형식으로 인접 리스트가 실행됩니다.
1) g->adj_list[n]은 List 형 구조체 포인터 입니다.
-> 즉, vx와 link를 참조할 수 있습니다.
2) g->adj_list[n]->vx = -1
g->adj_list[n]->link = NULL로 초기화 됩니다.
3) g->adj_list[n]->link에 연결될 정점의 정보가 추가됩니다.
ex) g->adj_list[u]->link = tmp_v (v 정점에 대한 정보를 포함하는 List 구조체 포인터)
위와 같은 방식으로 u, v에 각각 실행해주면 두 정점을 잇는 간선에 대한 정보가 저장됩니다.
void Add_Vertex(Graph* g){
g->adj_list[g->n] = (List*)malloc(sizeof(List));
g->adj_list[g->n]->vx = -1;
g->adj_list[g->n]->link = NULL;
g->n++;
}
void Add_Edge(Graph* g, int u, int v){
if(u >= g->n || v >= g->n){
printf("Out of Graph.\n\n");
}
else{
List* tmp_u = (List*)malloc(sizeof(List)); // u, v에 대한 정보를 저장하는 List 구조체 포인터를 생성합니다.
List* tmp_v = (List*)malloc(sizeof(List));
tmp_u->vx = u;
tmp_v->vx = v;
tmp_v->link = g->adj_list[u]->link; // 새로 연결될 정점의 link는 이전에 연결되어 있던 정점의 정보를 저장하고,
g->adj_list[u]->link = tmp_v; // 이전에 연결된 정점 자리로 연결됩니다.
// 기본적인거지만 이것만 확실히 인지하고 계시면 그래프, 리스트 등등 전부 편합니다.
// A->link = B 일 때, C를 A와 B에 추가로 연결하고 싶다면
// 1. C->link = A->link (== B)
// 2. A->link = C_link
// 3. 결과는 다음과 같습니다.
// A->link == C_link
// C->link == B
// 4. 즉, A->C->B 순서로 연결됩니다.
// 5. B->link = C를 해줄 수도 있습니다.
// 하지만, 대부분의 경우에 root 노드인 A와 새로 연결된 노드의 정보만을 이용하여 연결합니다.
// 즉, B->link에 대한 정보를 활용하기 불편하죠.. (처음은 괜찮지만 link->link->link 이런 식으로..)
// A, B, C의 순서가 중요한 것이 아닌 '연결'만 신경쓰시면 됩니다.
tmp_u->link = g->adj_list[v]->link;
g->adj_list[v]->link = tmp_u;
}
}
3. 정점 연결 확인
그래프에 추가된 정점 u와 v가 간선으로 이어져있는지 확인합니다.
애초에 간선을 생성할 때 두 정점의 인점 리스트에 모두 저장을 했으므로
하나의 정점에 대한 인접 리스트를 검사하여 연결 여부를 확인합니다.
void Check_Link(Graph* g, int u, int v){
if(u >= g->n || v >= g->n){
printf("Out of Graph.\n\n");
}
else{
List* cur;
List* tmp;
cur = g->adj_list[u]->link; // link에 가장 앞자리에 연결된 노드의 정보가 포합됩니다.
while(cur != NULL){ // 인접 리스트에 마지막으로 연결된 정점은 NULL과 Link로 연결됩니다.
tmp = cur->link;
if(cur->vx == v){
printf("Connected!! [%d]--[%d]\n", u, v);
return;
}
cur = tmp;
}
printf("Disconnected!! [%d]\\[%d]\n", u, v);
}
}
4. 정점 또는 간선을 삭제합니다.
Delete_Vertex
삭제하려면 우선 탐색을 해야합니다.
지금은 단순히 삭제하고 싶은 정점의 인접 리스트를 순차적으로 방문하며 동적 할당된 메모리를 해제합니다.
이때 BFS, DFS를 활용할 수도 있습니다.
Delete_Edge
삭제하고자 하는 간선과 연결된 두 정점의 인접 리스트에서 서로를 삭제합니다.
void Delete_Vertex(Graph* g, int u){
// 1. 모든 정점의 연결 리스트에서 u의 정보를 삭제합니다.
// 2. u의 인접 리스트에 연결된 모든 정점에 대한 정보를 삭제한다.
if(u >= g->n){
printf("Out of Graph.\n\n");
}
else{
List* cur;
List* pre;
List* tmp;
// 1. 모든 정점의 연결 리스트에서 u의 정보를 삭제합니다.
for(int i = 0; i < g->n && i != u; i++){
pre = g->adj_list[i]; // 삭제하고자 하는 정점의 앞 부분에 연결된 노드 정보를 저장합니다.
cur = pre->link; // 삭제하고자 하는 정점의 정보를 저장합니다.
while(cur != NULL){
tmp = cur->link;
if(cur->vx == u){ // 현재 노드 cur이 삭제하고자 하는 정점일 때
pre->link = cur->link; // 앞 부분의 노드를 cur 뒷 부분의 노드와 연결해주고
free(cur); // 본인은 삭제됩니다.
break;
}
pre = cur;
cur = tmp;
}
}
// 2. u의 인접 리스트에 연결된 모든 정점에 대한 정보를 삭제한다.
pre = g->adj_list[u]; // 지우고자 하는 정점의 인접 리스트입니다.
cur = g->adj_list[u]->link;
while(cur != NULL){ // 마지막 정점까지 이동하면서 할당된 메모리를 전부 해제해줍니다.
tmp = cur->link;
free(cur);
cur = tmp;
}
pre->link = NULL; // 마지막으로 지우고자 하는 인접 리스트의 가장 첫번째 자리를 NULL을 연결합니다.
}
}
void Delete_Edge(Graph* g, int u, int v){
// 서로의 인접 리스트에서 서로의 정보를 삭제합니다.
if(u >= g->n){
printf("Out of Graph.\n\n");
}
else{
List* cur;
List* pre;
List* tmp;
// 같은 것을
pre = g->adj_list[u];
cur = g->adj_list[u]->link;
while(cur != NULL){
tmp = cur->link;
if(cur->vx == v){
pre->link = cur->link;
free(cur);
break;
}
pre = cur;
cur = tmp;
}
// 두 번 반복합니다.
pre = g->adj_list[v];
cur = g->adj_list[v]->link;
while(cur != NULL){
tmp = cur->link;
if(cur->vx == u){
pre->link = cur->link;
free(cur);
break;
}
pre = cur;
cur = tmp;
}
}
}
5. 깊이 우선 탐색 (DFS: Deepth First Search)
두가지 탐색 방법 중 깊이 우선 탐색입니다.
깊이 우선 탐색이란 다음과 같습니다.
1) 시작 정점을 방문한다.
2) 시작 정점과 연결된 정점을 방문한다.
3) 그 정점과 연결된 정점을 방문한다.
4) 더 이상 연결된 정점이 없을 때까지 3)을 반복한다.
5) 3)에서 방문하기 전으로 돌아가서 연결된 다른 정점을 방문한다.
(A와 연결된 B를 방문했는데 B에 더이상 연결된 정점이 없다면, 다시 A로 돌아가서 A와 연결된 C를 방문합니다.)
6) 모든 정점에 대한 탐색이 종료될 때까지 3) ~ 5)를 반복한다.
void DFS(Graph *g, int n){
for(int i = 0; i < MAX_VERTEX; i++){
check[i] = 0; // 방문한 정점을 확인하기 위한 행렬을 초기화합니다.
}
Depth_First_Search(g, n);
printf("\n");
}
void Depth_First_Search(Graph* g, int n){
if(check[n] == 0){
List* cur;
List* tmp;
cur = g->adj_list[n]->link; // n번 정점을 방문합니다.
printf("%2d ", n);
check[n] = 1; // 정점의 방문 여부를 갱신합니다.
while(cur != NULL){ // 해당 노드와 연결된 정점이 더이상 없을 때까지 반복합니다.
tmp = cur->link;
if(check[cur->vx] == 0)
Depth_First_Search(g, cur->vx); // 연결된 정점을 방문해서 위의 과정을 반복합니다.
cur = tmp;
}
}
}
6. 넓이 우선 탐색 (BFS: Breath First Search)
넓이 우선 탐색은 다음과 같은 과정으로 진행됩니다.
1) 시작 정점을 방문합니다.
2) 시작 정점과 연결된 정점을 방문하고, 해당 정점이 방문하지 않은 정점일 때 큐에 저장합니다.
3) 연결된 정점이 없을 때까지 2)를 반복합니다.
4) 큐에 저장된 정점들에 대해 큐가 빌 때까지 위의 과정을 반복합니다.
해당 알고리즘에는 큐가 사용된다는 특징이 있습니다.
단순하게 말하자면 다음과 같습니다.
시작 정점과 연결된 정점을 쫙 방문하고, 연결된 정점을 순서대로 방문하며 각각 연결된 정점을 쫙 방문한다.
void BFS(Graph *g, int n){
for(int i = 0; i < MAX_VERTEX; i++){
check[i] = 0; // 정점 방문 여부를 확인하기 위한 행렬을 초기화합니다.
}
front = 0; // 큐를 사용하기 위해 관련 변수를 초기화합니다.
rear = 0;
Breath_First_Search(g, n);
printf("\n");
}
void Breath_First_Search(Graph* g, int n){
// 기준 노드와 연결된 노드 쫙 탐색, 연결된 노드에 연결된 노드를 차례대로 쫙 탐색
List* cur;
List* tmp;
int queue_out;
cur = g->adj_list[n]->link; // n번 정점과 연결된 첫번째 정점 cur을 확인합니다.
if(check[n] == 0){ // 방문하지 않았으면,
printf("%2d ", n); // 출력하고
check[n] = 1; // 방문했다고 갱신합니다.
}
while(cur != NULL){ // 이제 n번 정점과 연결된 모든 정점에 대해 탐색과 동시에 큐에 저장합니다.
tmp = cur->link;
if(check[cur->vx] == 0){ // 방문하지 않은 정점일 때, 출력과 함께 큐에 저장합니다.
printf("%2d ", cur->vx);
check[cur->vx] = 1;
Add_Queue(cur->vx);
}
cur = tmp;
}
queue_out = Delete_Queue(); // 큐에 저장된 정점을 출력합니다.
while(queue_out != -1){ // 큐에 더이상 정점이 없으면 -1을 출력합니다.
Breath_First_Search(g, queue_out); // 큐에서 출력된 정점에 대해 위의 과정을 반복합니다.
queue_out = Delete_Queue();
}
}
7. BFS를 사용하기 위한 큐를 정의합니다.
큐는 앞선 게시물을 참조해주세요.
원형 큐를 사용했습니다!!
void Add_Queue(int n){
if((rear+1)%MAX_QUEUE == front){
puts("Queue is full.");
}
else{
rear = (rear+1)%MAX_QUEUE;
queue[rear] = n; // 1번부터 찬다.
}
}
int Delete_Queue(void){
int tmp = -1;
if(front == rear){
// puts("Queue is empty.");
}
else{
front = (front+1)%MAX_QUEUE;
tmp = queue[front];
}
return tmp;
}
8. 전체 코드
//
// main.c
// Graph_New_BFS_DFS
//
// Created by 김경민 on 2020/05/11.
// Copyright © 2020 김경민. All rights reserved.
//
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERTEX 10
#define MAX_QUEUE MAX_VERTEX+1
int check[MAX_VERTEX];
/*-----------Graph-----------*/
typedef struct LIST {
int vx;
struct LIST* link;
}List;
typedef struct GRAPH {
int n;
List* adj_list[MAX_VERTEX];
}Graph;
/*---------------------------*/
/*---------Graph ADT---------*/
Graph* Init_Graph(void);
void Add_Vertex(Graph* g);
void Add_Edge(Graph* g, int u, int v);
void Check_Link(Graph* g, int u, int v);
void Delete_Vertex(Graph* g, int u);
void Delete_Edge(Graph* g, int u, int v);
void DFS(Graph *g, int n);
void Depth_First_Search(Graph* g, int n);
void BFS(Graph *g, int n);
void Breath_First_Search(Graph* g, int n);
void Add_Queue(int n);
int Delete_Queue(void);
/*---------------------------*/
/*-----------Queue-----------*/
int front = 0;
int rear = 0;
int queue[MAX_QUEUE];
/*---------------------------*/
int main(void) {
Graph* g = Init_Graph();
for(int i = 0; i < 5; i++){
Add_Vertex(g);
}
Add_Edge(g, 0, 1);
Add_Edge(g, 0, 2);
Add_Edge(g, 0, 3);
Add_Edge(g, 1, 2);
Add_Edge(g, 1, 3);
Add_Edge(g, 1, 4);
Check_Link(g, 1, 3);
#if 0
Delete_Vertex(g, 3);
Check_Link(g, 1, 3);
Check_Link(g, 3, 0);
#endif
#if 0
Delete_Edge(g, 1, 0);
Check_Link(g, 1, 0);
Check_Link(g, 0, 1);
#endif
DFS(g, 0);
BFS(g, 0);
return 0;
}
Graph* Init_Graph(void){
Graph* g = (Graph*)malloc(sizeof(Graph));
g->n = 0;
for(int i = 0; i < MAX_VERTEX; i++)
g->adj_list[i] = NULL;
return g;
}
void Add_Vertex(Graph* g){
g->adj_list[g->n] = (List*)malloc(sizeof(List));
g->adj_list[g->n]->vx = -1;
g->adj_list[g->n]->link = NULL;
g->n++;
}
void Add_Edge(Graph* g, int u, int v){
if(u >= g->n || v >= g->n){
printf("Out of Graph.\n\n");
}
else{
List* tmp_u = (List*)malloc(sizeof(List));
List* tmp_v = (List*)malloc(sizeof(List));
tmp_u->vx = u;
tmp_v->vx = v;
tmp_v->link = g->adj_list[u]->link;
g->adj_list[u]->link = tmp_v;
tmp_u->link = g->adj_list[v]->link;
g->adj_list[v]->link = tmp_u;
}
}
void Check_Link(Graph* g, int u, int v){
if(u >= g->n || v >= g->n){
printf("Out of Graph.\n\n");
}
else{
List* cur;
List* tmp;
cur = g->adj_list[u]->link;
while(cur != NULL){
tmp = cur->link;
if(cur->vx == v){
printf("Connected!! [%d]--[%d]\n", u, v);
return;
}
cur = tmp;
}
printf("Disconnected!! [%d]\\[%d]\n", u, v);
}
}
void Delete_Vertex(Graph* g, int u){
if(u >= g->n){
printf("Out of Graph.\n\n");
}
else{
List* cur;
List* pre;
List* tmp;
for(int i = 0; i < g->n && i != u; i++){
pre = g->adj_list[i];
cur = pre->link;
while(cur != NULL){
tmp = cur->link;
if(cur->vx == u){
pre->link = cur->link;
free(cur);
break;
}
pre = cur;
cur = tmp;
}
}
pre = g->adj_list[u];
cur = g->adj_list[u]->link;
while(cur != NULL){
tmp = cur->link;
free(cur);
cur = tmp;
}
pre->link = NULL;
}
}
void Delete_Edge(Graph* g, int u, int v){
if(u >= g->n){
printf("Out of Graph.\n\n");
}
else{
List* cur;
List* pre;
List* tmp;
pre = g->adj_list[u];
cur = g->adj_list[u]->link;
while(cur != NULL){
tmp = cur->link;
if(cur->vx == v){
pre->link = cur->link;
free(cur);
break;
}
pre = cur;
cur = tmp;
}
pre = g->adj_list[v];
cur = g->adj_list[v]->link;
while(cur != NULL){
tmp = cur->link;
if(cur->vx == u){
pre->link = cur->link;
free(cur);
break;
}
pre = cur;
cur = tmp;
}
}
}
void DFS(Graph *g, int n){
for(int i = 0; i < MAX_VERTEX; i++){
check[i] = 0;
}
Depth_First_Search(g, n);
printf("\n");
}
void Depth_First_Search(Graph* g, int n){
if(check[n] == 0){
List* cur;
List* tmp;
cur = g->adj_list[n]->link;
printf("%2d ", n);
check[n] = 1;
while(cur != NULL){
tmp = cur->link;
if(check[cur->vx] == 0)
Depth_First_Search(g, cur->vx);
cur = tmp;
}
}
}
void BFS(Graph *g, int n){
for(int i = 0; i < MAX_VERTEX; i++){
check[i] = 0;
}
front = 0;
rear = 0;
Breath_First_Search(g, n);
printf("\n");
}
void Breath_First_Search(Graph* g, int n){
List* cur;
List* tmp;
int queue_out;
cur = g->adj_list[n]->link;
if(check[n] == 0){
printf("%2d ", n);
check[n] = 1;
}
while(cur != NULL){
tmp = cur->link;
if(check[cur->vx] == 0){
printf("%2d ", cur->vx);
check[cur->vx] = 1;
Add_Queue(cur->vx);
}
cur = tmp;
}
queue_out = Delete_Queue();
while(queue_out != -1){
Breath_First_Search(g, queue_out);
queue_out = Delete_Queue();
}
}
void Add_Queue(int n){
if((rear+1)%MAX_QUEUE == front){
puts("Queue is full.");
}
else{
rear = (rear+1)%MAX_QUEUE;
queue[rear] = n; // 1번부터 찬다.
}
}
int Delete_Queue(void){
int tmp = -1;
if(front == rear){
// puts("Queue is empty.");
}
else{
front = (front+1)%MAX_QUEUE;
tmp = queue[front];
}
return tmp;
}
9. 실행결과

'Programming > C' 카테고리의 다른 글
| [자료구조 C 언어] C 프로그래밍 자료구조 - 18 : 그래프(4) 최단 거리 (shortest path) (1) | 2020.03.19 |
|---|---|
| [자료구조 C 언어] C 프로그래밍 자료구조 - 17 : 그래프(3) 최소 신장 트리 (MST): Kruskal, Prim 알고리즘 (0) | 2020.03.19 |
| [자료구조 C 언어] C 프로그래밍 자료구조 - 15 : 그래프(1) 기본 개념 (0) | 2020.03.18 |
| [자료구조 C 언어] C 프로그래밍 자료구조 - 14 : 이진 탐색 트리 (Binary Search Tree) (0) | 2020.03.18 |
| [자료구조 C 언어] C 프로그래밍 자료구조 - 13 : 힙 트리 (Heap Tree)와 우선 순위 큐 (Priority Queue) (0) | 2020.03.16 |