* 게시물에 사용된 그림 및 사진의 무단 도용을 금지합니다.
지난 게시물을 마지막으로 트리에 대한 내용을 마쳤습니다.
이번에는 그래프에 관한 내용을 설명드리겠습니다.
그래프는 트리를 포함하는 더 큰 집합입니다.
1. 그래프
그래프란 연결되어 있는 객체 간의 관계를 표현하는 자료구조 입니다.
예를 들어, 지하철 노선도, SNS 내의 친구 관계, 컴퓨터 네트워크 등이 있습니다.
저와 다른 유저들이 각각 객체이고, 저와 다른 유저가 팔로워인지 아닌지가 객체간의 관계가 되는 것입니다.
2. 그래프의 데이터 타입
그래프 G의 두 가지 구성 요소는 다음과 같습니다.
1) V(G): G에 포함된 정점(vertex)들의 집합
2) E(G): G에 포함된 간선 또는 에지 (edge)들의 집합
3) G = (V, E)라고 표기합니다.
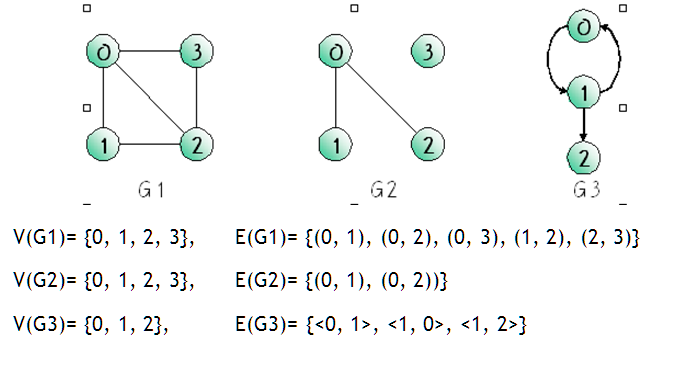
그래프는 각 객체간의 관계에 따라 다음과 같은 두 가지 종류로 나뉩니다.
1) 무방향성 그래프 (Undirected graph)
: Vertex의 쌍을 나타내는 edge가 방향성이 없음
: (u, v), (v, u) = 동일한 edge를 표현 (u, v는 각각 vertex)
2) 방향성 그래프 (Directed graph)
: 각 edge에 방향성이 존재하는 그래프
: <u, v> = u -> v인 edge를 표현 (u: tail, v: head)

3. 그래프 기본 용어
1) 완전 그래프 (Complete graph)
: Edge의 수가 최대인 그래프
: n개의 vertex -> 최대 egde 수 = n(n-1) / 2
2) 부분 그래프 (Subgraph)
: G' 그래프의 모든 노드와 엣지가 G의 노드 집합, 엣지 집합에 포함된다면 G'는 G의 부분 그래프이다.
3) 두 vertex u에서 v까지의 경로 (Path)
: 그래프의 에지를 통해 두 정점을 연결하는 통로
EX) 1부터 3까지의 경로 = (1, 3) (1, 0, 3) (1, 2, 0, 3)
4) 경로의 길이
: 경로 상에 있는 edge의 수
5) 단순 경로 (Simple path)
: 처음과 마지막을 제외한 vertex가 다른 경로
6) 사이클 (Cycle)
: 처음과 마지막이 동일한 단순 경로
7) 연결 (Connected)
: Vertex u와 v 사이에 경로가 존재할 경우, u와 v는 연결
: 방향성 그래프: strongly connected
8) 연결 요소 (Connected component)
: Maximal connected subgraph
: 방향성 그래프: strongly connected component
: 노드와 엣지가 서로 겹치지 않는 subgraph를 요소라고 합니다.
: 요소 가운데 요소 내 모든 노드 쌍에 대해 경로가 존재하는 subgraph를 연결 요소라고 합니다.
9) 트리
: 트리는 connected acyclic graph입니다.
: 즉, 연결되어 있고, 사이클이 아닌 그래프입니다.
10) Vertex의 차수 (Degree)
: v에 연결된 edge의 수
: 방향성 그래프에서 다음 두가지 차수가 존재합니다.
--> in-degree = v가 head가 되는 edge의 수
--> out-degree = v가 tail이 되는 edge의 수
11) Digraph
: Directed Graph의 준말
4. 그래프의 표현
인접 행렬 (Adjacency Matrix)와 인접 리스트 (Adjacency List) 방법이 있습니다.
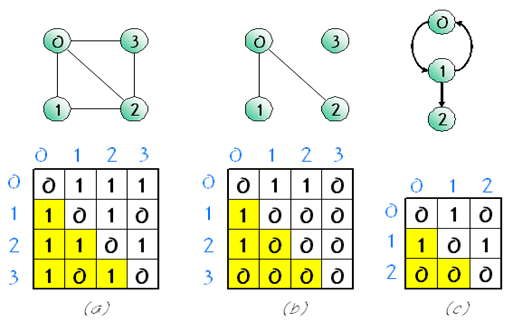
4-1. 인접 행렬 (Adjacency Matrix)
2차원 행렬로 그래프를 표현합니다.
1) 정점이 n 개일 경우: A[n][n]
--> (u, v)가 그래프 G의 edge 집합 E에 포함되면, A[u][v] = 1
--> 포함되지 않으면, A[u][v] = 0
2) 무방향성 그래프: A는 대칭 행렬
3) 방향성 그래프: A는 비대칭 행렬
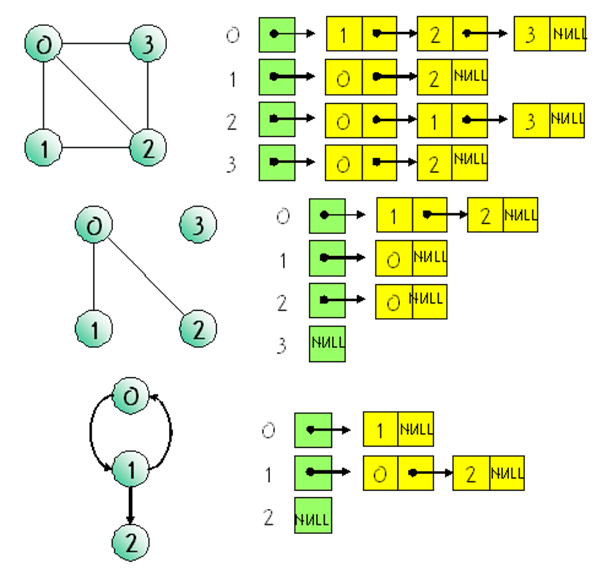
4-2. 인접 리스트 (Adjacency List)
인접 행렬의 n 행들을 n 개의 연결 리스트로 표현합니다.
즉, 그래프 G의 각 vertex에 대해 한 개의 연결 리스트가 존재합니다.
5. 그래프 표현 방법들의 분석
두가지의 표현 방법은 사용자가 목적하는 시스템의 성능과 크기에 따라 그 역할을 달리합니다.
1) G에 존재하는 edge의 수 계산, 혹은 G가 연결되었는 지 검사할 때
(n = vertex의 수, e = edge의 수)
1-1) 인접 행렬: n(n-1)/2 개의 항을 조사 = O(n^2)
1-2) 인접 리스트: O(n+e)
=> 만약, e << (n^2) / 2 일 때 인접 리스트가 더 효율적입니다.
2) Directed Graph에서 vertex의 in-degree를 조사할 때
2-1) 인접 행렬: O(n)
2-2) 인접 리스트: O(n+e)
-> 역인접 리스트 (inverse adjacency list)를 별도 유지해야합니다.