참고 1: https://gsmesie692.tistory.com/146
AOV/AOE Network를 이용한 작업 시간 구하기
얼마 전에 우연한 계기로 어떤 알고리즘 문제를 풀게 됐는데, 딱 보자마자 학부 시절 자료구조 시간에 배웠던 AOE Network와 Critical Path라는 개념이 떠올랐다. 그걸 이용해서 문제를 풀 수 있겠다는
gsmesie692.tistory.com
참고 2: http://www.kmooc.kr/asset-v1:YeungnamUnivK+YU216002+2016_02+type@asset+block@data_13-1_PPT.pdf
단순한 정리와 활용을 원하시는 분은 마지막 코드를 참조해주세요.
주석만으로도 충분히 이해하실 수 있습니다.
1. 작업 네트워크 (Activity Networks)
1) 작업 (Activity)
- 전체 프로젝트의 일부분
- 각각의 작업들이 완료되어야 전체 프로젝트가 성공적으로 완료
2) 네트워크
- AOV (Activity on Vertex) 네트워크
- AOE (Activity on Edge) 네트워크
2. AOV 네트워크
1) 특징
- 작업을 정점으로 표현한 방향성 그래프
- 간선은 작업들간의 선후 관계를 표현
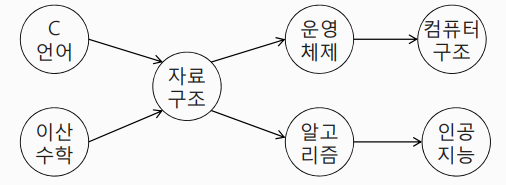
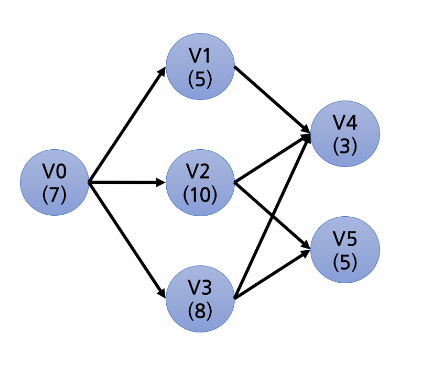
- V1이 시작되기 위해선 V0가 먼저 실행되어야 합니다.
- V4가 시작되기 위해선 V1 또는 V2 또는 V3가 먼저 실행되어야 합니다.
-> V0 - V1 = 7 + 5 = 12
-> V0 - V2 = 7 + 10 = 17
-> V0 - V3 = 7 + 8 = 15
=> V4가 가장 빨리 시작할 수 있는 시간 = 12
=> V4가 가장 늦게 시작할 수 있는 시간 = 17
2) 위상 정렬 (Topological Sort)
- 작업들간의 선후 관계를 유지하면서 모든 작업을 나열
- 작업의 나열 방법을 여러 개 존재 가능
-> 먼저 처리해야 하는 일부터 나열

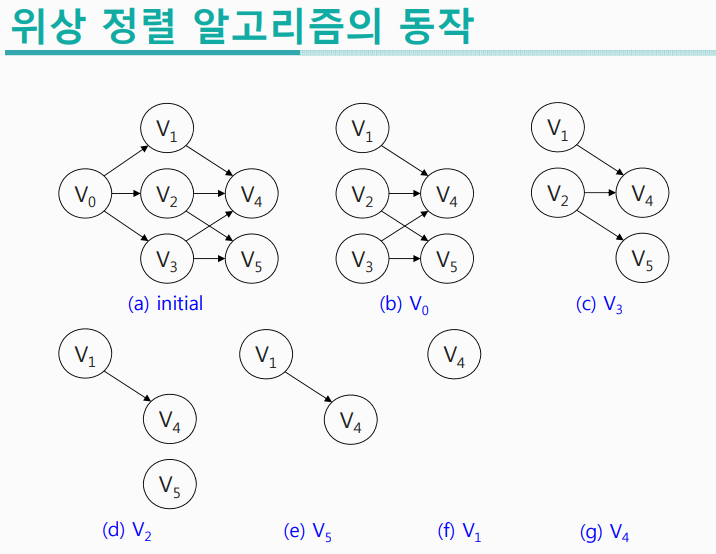

2-1. 네트워크의 표현
1) 인접 리스트로 표현
- 임의의 정점이 선행 정점을 갖는지 조사
- 각 정점에 대해 바로 앞의 선행 정점의 수를 나타내는 count field를 저장
-> 해당 정점으로 들어오는 간선의 수!!!
2) 위상 정렬 알고리즘
`- 삭제되는 간선에 연결된 정점의 count를 1 감소
- count가 0인 정점들은 스택이나 큐에 저장
-> 먼저 선행되어야 할 작업이 끝난 정점을 의미한다.
- 스택이나 큐에 저장된 정점이 소진될 때까지 아래 과정을 반복한다.
-> 스택이나 큐에서 출력된 정점이 연결된 정점의 count를 1 씩 감소시킨다.
-> count가 0인 정점들을 스택이나 큐에 저장한다.

3. AOE 네트워크
1) 방향성 그래프
- 간선은 작업을 표현 (가중치: 작업의 소요시간)
- 정점은 작업의 완료를 나타내는 사건(event)를 의미
-> 정점에서 나가는 작업(a1, a2, ..., a10)은 사건(v1, v2, ..., v8)이 발생하기 전까지 시작될 수 없다.
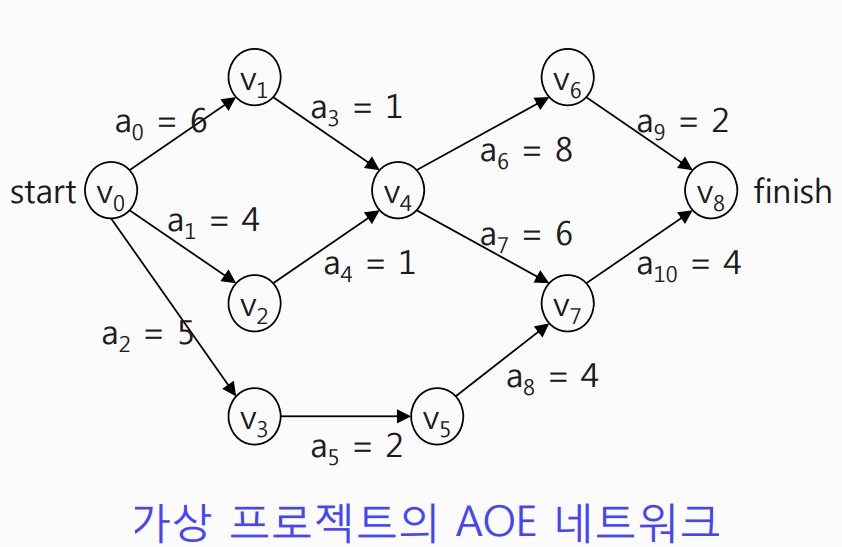
3-1. 임계 경로
1) 임계 경로 (Critical Path)
- 출발 정점에서 종료 정점까지 가장 긴 경로
- 임계 작업: 임계 경로에 포함된 작업
2) 임계 작업을 구하는 알고리즘
- 각 작업이 시작할 수 있는 가장 빠른 시간 (EST: Earliest Start Time)을 구한다.
(위의 그림을 예로든다.)
-> V4에 도달하기 위해선 V1과 V2가 선행되어야 한다.
-> V0 - V1 - V4 = 6 + 1 = 7
-> V0 - V2 - V4 = 4 + 1 = 5
=> V4가 시작될 수 있는 EST는 7이다.
=> 마찬가지로 V1과 V2의 EST는 각각 6, 4 입니다.
- 프로젝트 기간을 증가시키지 않으면서 작업이 시작될 수 있는 가장 나중 시간 (LST: Latest Start Time)을 구한다.
(프로젝트 기간은 모든 작업이 끝나는 시간을 기준으로 한다.)
-> V4가 마지막 작업일 때를 가정한다.
-> 위에서 구한 것과 같이 V2까지 아무리 빨리 끝내고 V4에 도달한다고 해도
-> V1가 남는다.
-> 따라서, 모든 작업을 마치는 것(V4에 도달하는 것)을 기준으로 할 때
-> V2은 7 - 5 = 2만큼 쉬었다 해도 전체 작업을 끝내는 시간에 변화가 없다.
=> V2의 LST는 4 (원래 V2까지 가는데 걸리는 시간) + 2 (V4로 가기전에 V1이 끝나는 걸 기다리면서 노는 시간) = 6
=> 마찬가지로 V1과 V4의 LST는 각각 6, 7 입니다.
- 위상 정렬 알고리즘을 이용하여 가장 빠른 시간과 가장 나중 시간을 계산한다.
- 임계 작업: 가장 빠른 시간 = 가장 나중 시간인 작업
=> 즉, V1과 V4는 임계 작업입니다.
- 임계 경로: 시작 정점부터 최종 정점까지의 가장 긴 경로의 길이이다.
-> 임계 경로의 소요시간이 곧 전체 작업이 다 끝나는데 필요한 최소 시간이 된다.
=> 실제 업무 시 임계 작업에 포함되지 않은 인력을 임계 작업으로 분배하여 업무 효율을 높일 수 있다.
=> 위의 예제에서 V2에서 2만큼 놀 수 있는 팀원을 V1에 보내면, V4까지 더 빨리 도달할 수 있겠죠?
4. 코드
4-1. 네트워크의 ADT
/*-----------ADT------------*/
void Init_Headnodes(void); // List롤 네트워크를 구성하기 위한 초기화를 진행합니다.
Node* Init_Vertex(int vertex); // 정점에 대한 정보를 저장하는 구조체 포인터를 동적할당합니다.
void Input_Head_2_Node(int u, int v); // 헤드 노드에 다른 노드를 연결합니다.
void Activity_On_Vertex(void); // AOV를 위상 정렬 합니다. (스택과 DFS를 사용)
void Cal_EST(void); // AOV에서 각 정점의 Earliest Start Time을 구합니다.
void Inverting_Graph(void); // 그래프의 인접 리스트를 역순으로 구성합니다.
void Cal_LST(void); // AOV에서 각 정점의 Latest Start Time을 구합니다.
/*--------------------------*/
4-2. 그래프 초기화 함수
Init_Headnodes
count = 헤드 노드가 다른 노드에 연결된 횟수를 저장
weight = 해당 노드의 작업 시간
EST = 해당 작업을 시작할 수 있는 가장 빠른 시간
LST = 해당 작업을 시작할 수 있는 가장 늦은 시간
link = 헤드 노드와 다른 노드를 연결하는 구조체 포인터
Init_Vertex
임의의 vertex 정보를 포함하는 Node 구조체 포인터를 생성하고 반환합니다.
Input_Head_2_Node
Init_Vertex에서 생성된 Node 구조체 포인터를 헤드 노드에 연결합니다.
void Init_Headnodes(void) {
for (int i = 0; i < MAX_VERTICES; i++) {
graph[i].count = 0;
graph[i].weight = 0;
graph[i].EST = 0;
graph[i].LST = 0;
graph[i].link = NULL;
}
}
Node* Init_Vertex(int vertex) {
Node* tmp = (Node*)malloc(sizeof(Node));
tmp->vertex = vertex;
tmp->link = NULL;
return tmp;
}
void Input_Head_2_Node(int u, int v) { // 헤드 노드에서 다른 노드로 가는 경로를 이어줍니다.
Node* cur = Init_Vertex(v);
Node* tmp;
tmp = graph[u].link; // tmp는 기존에 헤드 노드에 연결되어있던 노드입니다.
graph[u].link = cur; // 헤드 노드에 현재 이어주고자 하는 노드를 연결해주고
cur->link = tmp; // 현재 이어주고자 하는 노드 뒤에 기존에 헤드 노드에 연결되어 있던 노드를연결해줍니다.
graph[v].count++; // 연결이 된 정점의 count를 증가시켜준다.
// count는 해당 노드가 다른 노드에 연결된 갯수를 저장합니다.
// 즉, 헤드 노드 u가 아닌 헤드 노드 v의 count를 증가시켜줍니다.
}
void Inverting_Graph(void) {
// 그래프의 리스트를 역순으로 다시 정렬해줍니다.
// EX) 괄호 안은 count 입니다.
// 0 (0) -> 1 (1)
// 0 (0) -> 2 (1)
// Invert 하면 다음과 같습니다.
// 1 (0) -> 0 (1)
// 2 (0) -> 0 (2): 0이 두 번 찔렸으니까!
int u;
int i = 0;
int j;
Node* tmp;
Node* cur;
Node* tmp1;
for (i = 0; i < MAX_VERTICES; i++) {
cur = graph[i].link;
// 정점 i와 연결된 정점들을 하나씩 방문한다.
// 방문한 정점의 inverted_graph에 정점 i를 연결해준다.
while (cur != NULL) {
tmp = (Node*)malloc(sizeof(Node));
u = cur->vertex;
tmp->vertex = i;
tmp->link = NULL;
tmp1 = inverted_graph[u].link;
inverted_graph[u].link = tmp;
tmp->link = tmp1;
inverted_graph[i].count++;
cur = cur->link;
}
}
}
4-3. Stack
AOV를 위상 정렬할 때 사용됩니다.
위상 정렬할 때 시작 정점 부터 해당 정점과 연결된 정점을 방문하며 방문된 정점의 count를 1 씩 낮춰줍니다.
이때 방문된 정점을 Stack에 저장합니다.
/*--------Stack---------*/
int top = -1;
int stack[MAX_VERTICES];
void Input_Stack(int n) {
if (top == MAX_VERTICES) {
//printf("Stack is full\n");
}
else {
stack[++top] = n;
//printf("Input stack[%d] = %d\n", top, n);
}
}
int Delete_Stack(void) {
int n = -1;
if (top == -1) {
//printf("Stack is empty\n");
}
else {
n = stack[top--];
//printf("Deleted stack[%d] = %d\n", top + 1, n);
}
return n;
}
/*----------------------*/
4-3. AOV의 위상 정렬 알고리즘 (DFS, Stack 사용)
AOV를 위상 정렬 합니다.
아래의 절차에 따라 진행됩니다.
1) 시작 정점을 스택에 저장합니다.
2) 스택에 저장된 정점과 연결된 정점을 방문합니다.
3) 방문된 정점의 count를 1 감소시킵니다.
4) count가 0이 된 정점은 스택에 저장합니다.
5) 스택에 저장된 정점이 없을 때까지 1) ~ 4)를 반복합니다.
스택에 저장된 순서대로 출력하면, 위상 정렬의 결과를 확인할 수 있습니다.
void Activity_On_Vertex(void) { // aov 네트워크에 대한 위상 정렬을 실시합니다.
int i, j;
printf("AOV\n");
for (j = 0; j < MAX_VERTICES; j++) {
if (graph[j].count == 0) // count가 0인 것은 해당 노드 이전에 해야할 작업이 없다는 것을뜻합니다.
Input_Stack(j);
}
int n;
Node* tmp;
Node* cur;
while (top != -1) {
// 스택에 저장된 데이터가 없을 때까지 반복합니다.
n = Delete_Stack(); // 스택에 저장된 데이터를 하나 꺼내고
printf("%2d ", n);
cur = graph[n].link;
while (cur != NULL) {
// 해당 노드에 연결된 정점이 없을 때까지 반복합니다.
//printf("cur->vertex = %d\n", cur->vertex);
// 이게 스텍이 아니라면 순서가 반대로 출력될 것이다.
// 위상 정렬이란게 딱 한 순서만 있는게 아닌 듯 하다.
// 연결 리스트를 사용하므로 정점이 연결된 순서도 영향을 미친다.
graph[cur->vertex].count--; // 스택에서 나온 정점과 연결된 정점의 count를 감소 시킵니다.
if (graph[cur->vertex].count == 0) // 만약 연결된 노드의 count가 0이 되면 스택에입력해줍니다.
Input_Stack(cur->vertex); // 이 부분 때문에 가장 바깥 while문이 다시 한번반복됩니다.
cur = cur->link;
}
}
printf("\n\n");
}
4-4. Earliest Start Time 함수
AOV를 기준으로 EST를 구하는 알고리즘입니다.
특정 정점이 실행될 수 있는 제일 빠른 시간을 구합니다.
제일 빠른 시간의 개념을 헷갈리면 안 됩니다.
EX)
팀원들이 자료 조사를 다 해줘야 발표 자료를 만들 수 있을 때
다른 사람은 저녁 6시까지 자료 다 보내줬는데
한 놈이 저녁 10시에 보내면 저녁 10시가 '발표 자료 만들기'의 EST 입니다.
void Cal_EST(void) {
int i = 0;
Node* tmp;
Node* cur;
int max = 0;
while (i < MAX_VERTICES) { // 여기를 for문으로 구성해도 됩니다.
cur = graph[i].link;
//printf("111graph[%d].EST = %d\n", i, graph[i].EST);
while (cur != NULL) {
if (graph[cur->vertex].EST < graph[i].EST + graph[i].weight) { // i와 연결된 정점의 EST가 (i의 EST) + (i의 작업 시간) 보다 작을 때, i와 연결된 노드의 EST를 업데이트해준다.
graph[cur->vertex].EST = graph[i].EST + graph[i].weight;
//printf("222graph[%d].EST = %d\n", cur->vertex, graph[cur->vertex].EST);
if (graph[cur->vertex].EST >= max) {
max = graph[cur->vertex].EST; // 나중에 LST 계산을 위해 설정해줍니다.
}
}
cur = cur->link;
}
i++;
}
for (int j = 0; j < MAX_VERTICES; j++) {
//if (graph[j].EST == max) {
inverted_graph[j].LST = max; // LST는 EST의 max 보다 항상 작거나 같기 때문에 이와같이 초기화 합니다.
//printf("inverted_graph[%d].LST = %d\n", j, inverted_graph[j].LST);
//}
}
}
4-5. Lastest Start Time 함수
AOV의 역인접 리스트를 이용하여 LST를 계한합니다.
최대한 밍기적 거릴 수 있는 시간을 구합니다.
EX)
A, B, C가 숙제를 다 끝내야 D가 숙제를 끝내고 다 같이 치킨을 먹을 수 있다고 가정합니다.
숙제를 마치는데 A는 3일, B는 7일, C는 10일이 걸립니다.
어차피 10일이 지나야 D가 시작할 수 있습니다.
따라서 A는 10 - 3 = 7일 동안 놀다가 숙제를 시작해도 되고,
B는 10 - 7 = 3일 동안 놀다가 숙제를 해도 됩니다.
C는 10 - 10 = 0일.. 즉, 놀 시간이 없죠
위의 결과값이 각각의 LST입니다.
항상 마지막 작업의 EST는 곧 LST입니다. (마지막 작업(정점)의 EST == LST == 최대값)
그렇기 때문에 위에 EST를 구하는 함수에서 max를 구하고 모든 정점의 LST를 초기화 했습니다.
void Cal_LST(void) {
int i = MAX_VERTICES - 1; // 리스트의 가장 마지막 노드부터 시작합니다.
Node* cur;
for (; i >= 0; i--) { // EST와 if 문의 조건문과 역순으로 진행되는 것을 제외하고 모두 동일합니다.
cur = inverted_graph[i].link;
//printf("111inverted_graph[%d].LST = %d\n", i, inverted_graph[i].LST);
while (cur != NULL) {
int u = cur->vertex;
//printf("i = %d, u = %d\n", i, u);
if (inverted_graph[u].LST > inverted_graph[i].LST - inverted_graph[u].weight) {
inverted_graph[u].LST = inverted_graph[i].LST - inverted_graph[u].weight;
graph[u].LST = inverted_graph[u].LST;
}
//printf("222inverted_graph[%d].LST = %d\n", u, inverted_graph[u].LST);
graph[i].LST = inverted_graph[i].LST; // graph에도 LST 정보를 업데이트 하기 위함
cur = cur->link;
}
}
}
4-6. 전체 코드
AOV에 대한 위상 정렬과 EST, LST를 이용한 임계 경로, 임계 작업을 찾는 코드입니다.
// main.c
// Network_AoE_AoV
//
// Created by 김경민 on 2020/04/21.
// Copyright © 2020 김경민. All rights reserved.
//
// aov와 aoe를 활용한 임계 작업 시간 검색 방법을 구현한다
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERTICES 6
#define MIN(a, b) (((a) < (b)) ? (a) : (b))
#define MAX(a, b) (((a) > (b)) ? (a) : (b))
typedef struct NODE { // 헤드노드에 연결되는 노드 데이터를 저장합니다.
int vertex;
struct NODE* link;
}Node;
typedef struct HEADNODES { // 헤드노드에 대한 데이터를 저장합니다.
int count;
int weight;
int EST; // 작업을 시작할 수 있는 가장 빠른 시간입니다.
int LST; // 작업을 시작할 수 있는 가장 느린 시간입니다.
Node* link;
} Headnodes;
Headnodes graph[MAX_VERTICES];
Headnodes inverted_graph[MAX_VERTICES];
/*-----------ADT------------*/
void Init_Headnodes(void);
Node* Init_Vertex(int vertex);
void Input_Head_2_Node(int u, int v);
void Activity_On_Vertex(void);
void Cal_EST(void);
void Inverting_Graph(void);
void Cal_LST(void);
/*--------------------------*/
void Init_Headnodes(void) {
for (int i = 0; i < MAX_VERTICES; i++) {
graph[i].count = 0;
graph[i].weight = 0;
graph[i].EST = 0;
graph[i].link = NULL;
}
}
Node* Init_Vertex(int vertex) {
Node* tmp = (Node*)malloc(sizeof(Node));
tmp->vertex = vertex;
tmp->link = NULL;
return tmp;
}
void Input_Head_2_Node(int u, int v) { // 헤드 노드에서 다른 노드로 가는 경로를 이어줍니다.
Node* cur = Init_Vertex(v);
Node* tmp;
tmp = graph[u].link; // tmp는 기존에 헤드 노드에 연결되어있던 노드입니다.
graph[u].link = cur; // 헤드 노드에 현재 이어주고자 하는 노드를 연결해주고
cur->link = tmp; // 현재 이어주고자 하는 노드 뒤에 기존에 헤드 노드에 연결되어 있던 노드를연결해줍니다.
graph[v].count++; // 연결이 된 정점의 count를 증가시켜준다.
// count는 해당 노드가 다른 노드에 연결된 갯수를 저장합니다.
// 즉, 헤드 노드 u가 아닌 헤드 노드 v의 count를 증가시켜줍니다.
}
void Inverting_Graph(void) {
// 그래프의 리스트를 역순으로 다시 정렬해줍니다.
// EX) 괄호 안은 count 입니다.
// 0 (0) -> 1 (1)
// 0 (0) -> 2 (1)
// Invert 하면 다음과 같습니다.
// 1 (0) -> 0 (1)
// 2 (0) -> 0 (2): 0이 두 번 찔렸으니까!
int u;
int i = 0;
int j;
Node* tmp;
Node* cur;
Node* tmp1;
for (i = 0; i < MAX_VERTICES; i++) {
cur = graph[i].link;
// 정점 i와 연결된 정점들을 하나씩 방문한다.
// 방문한 정점의 inverted_graph에 정점 i를 연결해준다.
while (cur != NULL) {
tmp = (Node*)malloc(sizeof(Node));
u = cur->vertex;
tmp->vertex = i;
tmp->link = NULL;
tmp1 = inverted_graph[u].link;
inverted_graph[u].link = tmp;
tmp->link = tmp1;
inverted_graph[i].count++;
cur = cur->link;
}
}
}
/*--------Stack---------*/
int top = -1;
int stack[MAX_VERTICES];
void Input_Stack(int n) {
if (top == MAX_VERTICES) {
//printf("Stack is full\n");
}
else {
stack[++top] = n;
//printf("Input stack[%d] = %d\n", top, n);
}
}
int Delete_Stack(void) {
int n = -1;
if (top == -1) {
//printf("Stack is empty\n");
}
else {
n = stack[top--];
//printf("Deleted stack[%d] = %d\n", top + 1, n);
}
return n;
}
/*----------------------*/
void Activity_On_Vertex(void) { // aov 네트워크에 대한 위상 정렬을 실시합니다.
int i, j;
printf("AOV\n");
for (j = 0; j < MAX_VERTICES; j++) {
if (graph[j].count == 0) // count가 0인 것은 해당 노드 이전에 해야할 작업이 없다는 것을뜻합니다.
Input_Stack(j);
}
int n;
Node* tmp;
Node* cur;
while (top != -1) {
// 스택에 저장된 데이터가 없을 때까지 반복합니다.
n = Delete_Stack(); // 스택에 저장된 데이터를 하나 꺼내고
printf("%2d ", n);
cur = graph[n].link;
while (cur != NULL) {
// 해당 노드에 연결된 정점이 없을 때까지 반복합니다.
//printf("cur->vertex = %d\n", cur->vertex);
// 이게 스텍이 아니라면 순서가 반대로 출력될 것이다.
// 위상 정렬이란게 딱 한 순서만 있는게 아닌 듯 하다.
// 연결 리스트를 사용하므로 정점이 연결된 순서도 영향을 미친다.
graph[cur->vertex].count--; // 스택에서 나온 정점과 연결된 정점의 count를 감소 시킵니다.
if (graph[cur->vertex].count == 0) // 만약 연결된 노드의 count가 0이 되면 스택에입력해줍니다.
Input_Stack(cur->vertex); // 이 부분 때문에 가장 바깥 while문이 다시 한번반복됩니다.
cur = cur->link;
}
}
printf("\n\n");
}
void Cal_EST(void) {
// AOV를 기준으로 EST를 구하는 알고리즘입니다.
// 특정 정점이 실행될 수 있는 제일 빠른 시간을 구합니다.
// 제일 빠른 시간을 헷갈리면 안 됩니다.
// 팀원들이 자료 조사를 다 해줘야 발표 자료를 만들 수 있을 때
// 다른 사람은 저녁 6시까지 자료 다 보내줬는데
// 한 놈이 저녁 10시에 보내면 저녁 10시가 '발표 자료 만들기'의 EST 입니다.
int i = 0;
Node* tmp;
Node* cur;
int max = 0;
while (i < MAX_VERTICES) { // 여기를 for문으로 구성해도 됩니다.
cur = graph[i].link;
//printf("111graph[%d].EST = %d\n", i, graph[i].EST);
while (cur != NULL) {
if (graph[cur->vertex].EST < graph[i].EST + graph[i].weight) { // i와 연결된 정점의 EST가 (i의 EST) + (i의 작업 시간) 보다 작을 때, i와 연결된 노드의 EST를 업데이트해준다.
graph[cur->vertex].EST = graph[i].EST + graph[i].weight;
//printf("222graph[%d].EST = %d\n", cur->vertex, graph[cur->vertex].EST);
if (graph[cur->vertex].EST >= max) {
max = graph[cur->vertex].EST; // 나중에 LST 계산을 위해 설정해줍니다.
}
}
cur = cur->link;
}
i++;
}
for (int j = 0; j < MAX_VERTICES; j++) {
//if (graph[j].EST == max) {
inverted_graph[j].LST = max; // LST는 EST의 max 보다 항상 작거나 같기 때문에 이와같이 초기화 합니다.
//printf("inverted_graph[%d].LST = %d\n", j, inverted_graph[j].LST);
//}
}
}
void Cal_LST(void) {
// AOV의 역인접 리스트를 이용하여 LST를 계한합니다.
// 최대한 밍기적 거릴 수 있는 시간을 구합니다.
// 예를들어 A, B, C가 숙제를 다 끝내야 D가 숙제를 끝내고 다 같이 치킨을 먹을 수 있다고 가정합니다.
// 숙제를 마치는데 A는 3일, B는 7일, C는 10일이 걸립니다.
// 어차피 10일이 지나야 D가 시작할 수 있습니다.
// 따라서 A는 10 - 3 = 7일 동안 놀다가 숙제를 시작해도 되고,
// B는 10 - 7 = 3일 동안 놀다가 숙제를 해도 됩니다.
// C는 10 - 10 = 0일.. 즉, 놀 시간이 없죠
// 위의 결과값이 각각의 LST입니다.
// 항상 마지막 작업의 EST는 곧 LST입니다. (마지막 작업(정점)의 EST == LST == 최대값)
// 그렇기 때문에 위에 EST를 구하는 함수에서 max를 구하고 초기화 했습니다.
int i = MAX_VERTICES - 1; // 리스트의 가장 마지막 노드부터 시작합니다.
Node* cur;
for (; i >= 0; i--) { // EST와 if 문의 조건문과 역순으로 진행되는 것을 제외하고 모두 동일합니다.
cur = inverted_graph[i].link;
//printf("111inverted_graph[%d].LST = %d\n", i, inverted_graph[i].LST);
while (cur != NULL) {
int u = cur->vertex;
//printf("i = %d, u = %d\n", i, u);
if (inverted_graph[u].LST > inverted_graph[i].LST - inverted_graph[u].weight) {
inverted_graph[u].LST = inverted_graph[i].LST - inverted_graph[u].weight;
graph[u].LST = inverted_graph[u].LST;
}
//printf("222inverted_graph[%d].LST = %d\n", u, inverted_graph[u].LST);
graph[i].LST = inverted_graph[i].LST; // graph에도 LST 정보를 업데이트 하기 위함
cur = cur->link;
}
}
}
int main(void) {
// 가중치를 설정해붑니다.
// 이부분을 다른 그래프 함수에 사용된 랜덤 변수로 설정하셔도 됩니다.
graph[0].weight = 7;
graph[1].weight = 5;
graph[2].weight = 10;
graph[3].weight = 8;
graph[4].weight = 3;
graph[5].weight = 5;
for (int j = 0; j < MAX_VERTICES; j++) {
inverted_graph[j].count = 0;
inverted_graph[j].weight = graph[j].weight;
inverted_graph[j].link = NULL;
inverted_graph[j].LST = 0;
}
// 노드를 연결해줍니다.
// 마찬가지로 랜덤 변수를 사용할 수 있을 것 같습니다.
Input_Head_2_Node(0, 3);
Input_Head_2_Node(0, 2);
Input_Head_2_Node(0, 1);
Input_Head_2_Node(1, 4);
Input_Head_2_Node(2, 4);
Input_Head_2_Node(2, 5);
Input_Head_2_Node(3, 4);
Input_Head_2_Node(3, 5);
Inverting_Graph();
/* AOV의 위상정렬 */
Activity_On_Vertex();
puts("");
/* AOV를 이용한 Critical Path 찾기 */
Cal_EST();
Cal_LST();
for (int i = 0; i < MAX_VERTICES; i++) {
printf("graph[%2d].est = %2d, graph[%2d].lst = %2d", i, graph[i].EST, i, graph[i].LST);
if (graph[i].EST == graph[i].LST)
printf(" => vertex[%2d] is critical activity.", i);
printf("\n");
}
return 0;
}
5. 실행 결과

'Programming > C' 카테고리의 다른 글
| [자료구조 C 언어] 부록 - 2: 최소비용 신장트리 MST_Prim 알고리즘 (0) | 2020.05.14 |
|---|---|
| [자료구조 C 언어] 부록 - 1: 최소비용 신장트리 MST_Kruskal 알고리즘 (0) | 2020.05.13 |
| [자료구조 C 언어] C 프로그래밍 자료구조 - 18 : 그래프(4) 최단 거리 (shortest path) (1) | 2020.03.19 |
| [자료구조 C 언어] C 프로그래밍 자료구조 - 17 : 그래프(3) 최소 신장 트리 (MST): Kruskal, Prim 알고리즘 (0) | 2020.03.19 |
| [자료구조 C 언어] C 프로그래밍 자료구조 - 16 : 그래프(2) 기초 연산: 깊이 우선 탐색, 넓이 우선 탐색 등 (0) | 2020.03.19 |