1. Dijkstra 알고리즘
해당 알고리즘은 단일 출발점 문제의 해를 구합니다.
즉, 하나의 출발점으로부터 그래프 내의 모든 정점에 대한 최단 경로를 구합니다.
choose
모든 정점 중에서 아직 시작 정점과의 최단 거리가 결정되지 않고, 시작 정점 (출발점)과의 거리가 가장 짧은 정점을 반환합니다.
Shortest_Path_Dijkstra
choose에서 반환된 정점을 최단 거리가 결정되었다고 갱신합니다.
해당 정점을 기준으로 모든 정점에 대해 시작 정점과의 거리를 갱신합니다.
-> 반환된 정점을 경유하는게 빠른지 아닌지
int choose(int distance[], int n, int found[]) {
int min;
int min_pos;
min = INT_MAX;
min_pos = -1;
for (int i = 0; i < n; i++) {
if (distance[i] < min && found[i] == FALSE) {
min = distance[i];
min_pos = i;
}
}
return min_pos;
}
void Shortest_Path_Dijkstra(int start, int n) {
// Dijkstra 알고리즘으로 최단 경로를 구한다.
// 시작 정점으로부터 그래프 내의 모든 정점에 대한 최단 경로를 구합니다.
for (int i = 0; i < n; i++) {
distance[i] = weight[start][i]; // 시작 정점에서 다른 정점으로 향하는 가중치를 기준으로 초기화합니다.
found[i] = FALSE;
}
found[start] = TRUE; // 시작점은 그래프에 추가되었다고 가정하기 때문에
// 시작점의 방문 여부를 갱신해줍니다.
for (int i = 0; i < n - 1; i++) {
int u = choose(distance, n, found);
// 최단 거리가 결정되지 않고, 시작 정점과의 거리가 가장 짧은 정점을 반환합니다.
found[u] = TRUE; // 해당 정점의 최단 경로를 발견했다고 갱신합니다..
printf("%d is added to the Graph\n\n", u);
for (int j = 0; j < n; j++) {
if (found[j] == FALSE) { // 최단 경로를 발견하지 못 한 정점에 대해
if (distance[u] + weight[u][j] < distance[j]) {
// 시작 정점에서 j로 바로 가는게 빠를지, u를 경유해서 가는게 빠를지 판단 합니다.
printf("Before_distance update via[%d]: distance[%d] = %d\n", u, j, distance[j]);
distance[j] = distance[u] + weight[u][j];
printf("After_distance update via[%d]: distance[%d] = %d\n\n", u, j, distance[j]);
}
}
}
}
}
2. Floyd 알고리즘
모든 정점에 대해 각 정점 간의 최단 경로를 찾습니다.
아래 주석을 확인해주시면 되겠습니다.
void Shortest_Path_Floyd(void) {
// Floyd 알고리즘으로 최단 경로를 구한다.
// 해당 알고리즘은 모든 정점간의 최다 경로를 구합니다.
for (int u = 0; u < MAX_VERTICES; u++) {
for (int v = 0; v < MAX_VERTICES; v++) {
d[u][v] = weight[u][v];
}
}
for (int m = 0; m < MAX_VERTICES; m++) { // m이 경유하는 기준 정점이 됩니다.
for (int i = 0; i < MAX_VERTICES; i++) {
for (int j = 0; j < MAX_VERTICES; j++) {
if (d[i][j] > d[i][m] + d[m][j]) {
// 모든 정점 i와 j에 대해
// i에서 j로 바로 가는게 빠를지, m을 경유해서 가는게 빠를지 판단합니다.
// m을 경유해서 가는게 빠르다면,
// d[i][j] 갱신 후의 의미는 i->m->j를 내포합니다.
printf("Before_distance update via[%d]: distance[%d][%d] = %d\n", m, i, j, d[i][j]);
d[i][j] = d[i][m] + d[m][j];
printf("After_distance update via[%d]: distance[%d][%d] = %d\n\n", m, i, j, d[i][j]);
}
}
}
}
}
3. 전체 코드
// main.c
// Graph_Shortest_Path_Daijkstra_And_Floyd
//
// Created by 김경민 on 2020/04/20.
// Copyright © 2020 김경민. All rights reserved.
//
// 최단 경로 탐색 알고리즘을 구현한다.
// choose 함수에 우선 순위 큐를 사용하면 효율을 높일 수 있다.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>
#define INT_MAX 2147483647 // 최대 정수
#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 7 // 정점의 수
#define INF 1000 // 무한대 (연결이 없는 경우)
int weight[MAX_VERTICES][MAX_VERTICES] = {
{0,7,INF,INF,3,10,INF},
{7,0,4,10,2,6,INF},
{INF,4,0,2,INF,INF,INF},
{INF,10,2,0,11,9,4},
{3,2,INF,11,0,INF,5},
{10,6,INF,9,INF,0,INF},
{INF,INF,INF,4,5,INF,0}
};
//int weight[MAX_VERTICES][MAX_VERTICES] = {
// {0,1,8,INF},
// {1,0,7,2},
// {8,7,0,3},
// {INF,2,3,0}
//};
/* Dijkstra 변수*/
int distance[MAX_VERTICES];
int found[MAX_VERTICES];
/* Floyd 변수*/
int d[MAX_VERTICES][MAX_VERTICES];
int choose(int distance[], int n, int found[]) {
int min;
int min_pos;
min = INT_MAX;
min_pos = -1;
for (int i = 0; i < n; i++) {
if (distance[i] < min && found[i] == FALSE) {
min = distance[i];
min_pos = i;
}
}
return min_pos;
}
void Shortest_Path_Dijkstra(int start, int n) {
// Dijkstra 알고리즘으로 최단 경로를 구한다.
// 시작 정점으로부터 그래프 내의 모든 정점에 대한 최단 경로를 구합니다.
for (int i = 0; i < n; i++) {
distance[i] = weight[start][i]; // 시작 정점에서 다른 정점으로 향하는 가중치를 기준으로 초기화합니다.
found[i] = FALSE;
}
found[start] = TRUE;
for (int i = 0; i < n - 1; i++) {
int u = choose(distance, n, found);
// 최단 경로가 발견되지 않고, 시작 정점과의 거리가 가장 짧은 정점을 반환합니다.
found[u] = TRUE; // 해당 정점을 그래프에 포합합니다.
printf("%d is added to the Graph\n\n", u);
for (int j = 0; j < n; j++) {
if (found[j] == FALSE) {
if (distance[u] + weight[u][j] < distance[j]) {
// 시작 정점에서 j로 바로 가는게 빠를지, u를 경유해서 가는게 빠를지 판단 합니다.
printf("Before_distance update via[%d]: distance[%d] = %d\n", u, j, distance[j]);
distance[j] = distance[u] + weight[u][j];
printf("After_distance update via[%d]: distance[%d] = %d\n\n", u, j, distance[j]);
}
}
}
}
}
void Shortest_Path_Floyd(void) {
// Floyd 알고리즘으로 최단 경로를 구한다.
// 해당 알고리즘은 모든 정점간의 최다 경로를 구합니다.
for (int u = 0; u < MAX_VERTICES; u++) {
for (int v = 0; v < MAX_VERTICES; v++) {
d[u][v] = weight[u][v];
}
}
for (int m = 0; m < MAX_VERTICES; m++) { // m이 경유하는 기준 정점이 됩니다.
for (int i = 0; i < MAX_VERTICES; i++) {
for (int j = 0; j < MAX_VERTICES; j++) {
if (d[i][j] > d[i][m] + d[m][j]) {
// 모든 정점 i와 j에 대해
// i에서 j로 바로 가는게 빠를지, m을 경유해서 가는게 빠를지 판단합니다.
// m을 경유해서 가는게 빠르다면,
// d[i][j] 갱신 후의 의미는 i->m->j를 내포합니다.
printf("Before_distance update via[%d]: distance[%d][%d] = %d\n", m, i, j, d[i][j]);
d[i][j] = d[i][m] + d[m][j];
printf("After_distance update via[%d]: distance[%d][%d] = %d\n\n", m, i, j, d[i][j]);
}
}
}
}
}
int main(void) {
/* Dijkstra */
#if 0
Shortes_tPath_Dijkstra(0, MAX_VERTICES);
#endif
/* Floyd*/
#if 1
Shortest_Path_Floyd();
#endif
printf("\n");
return 0;
}
4. 실행 결과
1) Dijkstra
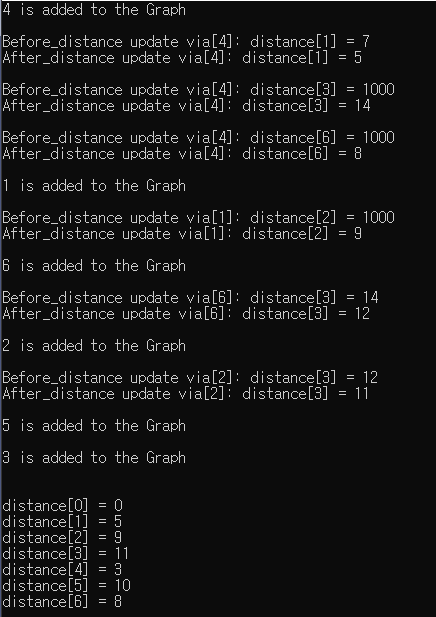
2) Floyd
그래프의 모든 정점 쌍에 대한 최단 경로를 구하기 때문에
출력 갯수가 많습니다. (n * n)

'Programming > C' 카테고리의 다른 글
| [자료구조 C 언어] 부록 - 2: 최소비용 신장트리 MST_Prim 알고리즘 (0) | 2020.05.14 |
|---|---|
| [자료구조 C 언어] 부록 - 1: 최소비용 신장트리 MST_Kruskal 알고리즘 (0) | 2020.05.13 |
| [자료구조 C 언어] C 프로그래밍 자료구조 - 19 : 네트워크 (AOV, AOE, EST, LST, critical path) (0) | 2020.03.19 |
| [자료구조 C 언어] C 프로그래밍 자료구조 - 18 : 그래프(4) 최단 거리 (shortest path) (1) | 2020.03.19 |
| [자료구조 C 언어] C 프로그래밍 자료구조 - 17 : 그래프(3) 최소 신장 트리 (MST): Kruskal, Prim 알고리즘 (0) | 2020.03.19 |