이진 트리를 활용한 알고리즘 중에 하나인 스레드 이진 트리에 대해서 알아보겠습니다.
많이 찾아봤는데 스레드 이진 트리는 자동으로 데이터를 입력하고 각 노드의 링크가 연결되는 코드를 찾기 힘들어서
제가 만들었습니다... 다른 자료는 대부분 초기 설정 값을 주고 시작하더라구요. (각 노드의 데이터와 링크를 수동으로 입력해서)
논리 구조를 제대로 이해하신다면 이해하기 어렵지 않을 겁니다.
코드만 보고 싶으신 분은 아래 /* 코드 설명 시작 */으로 내려가시면 됩니다.
이진 트리를 구성 할 때 제일 마지막 단에 있는 노드의 링크는 자식 노드가 없기 때문에 NULL을 가리키고 있습니다.
어차피 해당 링크의 메모리는 할당되어 있기 때문에 잉여 메모리를 활용하지 못 하는 비효율성을 해결하기 위해
도입된 개념이 스레드 이진 트리 입니다.
1. 스레드 이진 트리는 크게 두 가지의 장점을 가지고 있습니다
1). 트리 전체의 모든 링크를 활용한다.
2). 중위 순회의 편의성이 증대된다.
2.스레드 이진 트리는 다음과 같은 특징을 가집니다.
1). 트리의 노드는 순서대로 채워진다.
2). 자식 노드와 연결되지 않는 링크는 중위 선행자 (Inorder Predecessor) 또는 중위 후행자 (Inoder Successor)와 연결된다.
3). 중위 선행자 또는 중위 후행자가 없는 노드의 링크는 가상의 노드 head를 가리킨다.
여기서 다른 이진 트리와 다른 중요한 특징 중 하나는 head 노드입니다.
3.head 노드의 특징은 다음과 같습니다.
1). head 노드의 왼쪽 링크는 root 노드를 가리킨다. (root 노드는 이진 트리의 첫번째 노드입니다.)
2). head 노드의 오른쪽 링크는 head, 즉, 자기 자신을 가리킵니다.
3). head 노드에 저장된 데이터는 없습니다.
4). head를 제외한 이진 트리를 중위 순회 할 때 첫번쨰 노드의 왼쪽 링크와 마지막 노드의 오른쪽 링크는 head를 가립니다.
기본적인 개념은 여기서 끝입니다.
아래 그림과 함께 확인해보겠습니다.

이진 스레드 트리의 노드는 다음과 같은 구조체로 설정됩니다
typedef struct NODE{
char data;
struct NODE *left_child;
struct NODE *right_child;
int left_thread;
int right_thread;
} Node;
기존 이진 트리의 구조체에서 left_thread와 right_thread가 추가된 것을 확인하실 수 있습니다.
left_thread와 right_thread는
해당 노드의 링크가 자식을 가리키고 있을 때 FALSE (== 0),
중위 선행자 or 중위 후행자를 가리키고 있을 때 TRUE (== 1)가 됩니다
1. left_child = 왼쪽 자식 노드 --> left_thread = FALSE
1-1. left_child = 중위 선행자 --> left_thread = TRUE
2. right_child = 오른쪽 자식 노드 --> right_thread = FALSE
2-1. right_child = 중위 후행자 --> right_thread = TRUE
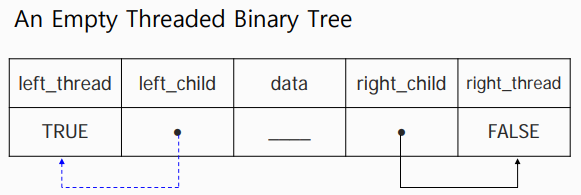
앞 서 설명드렸던 head 노드의 특징대로 초기화 되어 있는 것을 확인하실 수 있습니다.
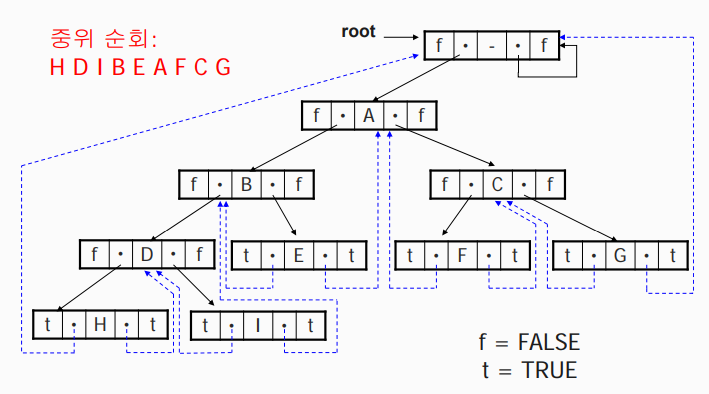
스레드 이진 트리의 구성은 위와 같습니다.
스레드 이진 트리의 가장 대표적인 함수는 insucc과 tinorder이 있습니다.
1. insucc : 원하는 노드의 중위 후행자를 찾아준다.

2. tinorder : head 노드부터 시작하여 이진 스레드 트리를 중회 순행하며 출력해준다.

/* 코드 설명 시작 */
이제 본격적으로 실제 스레드 이진 트리를 구현한 코드를 확인해보겠습니다.
1. 스레드 이진 트리의 ADT
Node *Init_Tree(void) : 트리 구조체 변수를 초기화 합니다.
void In_Order_Traverse_Predecessor(Node *thtr, char data) : 원하는 노드의 중위 선행자를 찾아줍니다.
void In_Order_Traverse_Successor(Node *thtr, char data) : 원하는 노드의 중위 후행자를 찾아줍니다.
void Find_Suc_Pre(Node *thtr, char data) : 위의 두 함수를 내부에 포함하고 있습니다. 원하는 노드의 중위 선행자와 후행자를 찾아줍니다.
void Input_Data(Thtr *tr, char data) : 원하는 데이터가 저장된 노드를 트리에 추가합니다.
Node *InPred(Node *tr) : 원하는 노드의 중위 선행자를 찾아줍니다. (노드가 구성된 뒤 실행될 수 있습니다.)
Node *InSucc(Node *tr) : 원하는 노드의 중위 후행자를 찾아줍니다. (노드가 구성된 뒤 실행될 수 있습니다.)
void TinOrder(Node *tr) : 트리를 중위 순회하며 출력해줍니다.
2. 스레드 이진 트리의 구현
배열 (구조체 배열)을 사용해 이진 트리를 구현할 때 항상 처음 노드의 인덱스는 1로 합니다.
2-1. 구조체 선언
2-2. 구조체 초기화
Node *Init_Tree(void){ // 구조체 변수를 초기화 해줍니다.
Node *tr = (Node *)malloc(sizeof(Node));
tr->data = 0; // char 데이터는 0을 저장할 때와 '0'가 다릅니다. (0 == NULL)
tr->left_child = NULL;
tr->right_child = NULL;
tr->left_thread = FALSE;
tr->right_thread = FALSE;
return tr; // 메모리가 동적할당된 구조체 포인터 변수의 주소값을 반환해줍니다.
}
2-3. 중위 선행자, 중위 후행자 탐색 (트리 구성 전, 후 모두 가능)
기본적으로 특정 노드의 중위 선행자는 '특정 노드의 왼쪽 서브트리 가장 오른쪽에 있다.'를 기억하시면 됩니다.
void In_Order_Traverse_Predecessor(Node *thtr, char data){ // 특정 데이터를 가진 노드의 중위 선행자를 찾아 pre에 저장합니다.
if(thtr){ // 해당 노드에 저장된 주소가 NULL일 경우 (저장된 데이터가 없는 경우) 조건문은 거짓이되어 if문이 실행되지 않습니다.
if(thtr->left_thread == FALSE){ // 해당 링크가 중위 선행자와 연결되어 있지 않을 때만 실행됩니다.
In_Order_Traverse_Predecessor(thtr->left_child, data);
}
if(sig == 0 && thtr->data != data){ // 특정 데이터를 가진 노드와 동일한 노드가 아닐 때 항상 저장됩니다.
pre = thtr;
}
else if(sig == 0 && thtr->data == data){ // 특정 데이터를 가진 노드를 발견했을 때 pre에 더이상 노드가 저장되지 않습니다.
sig = 1;
}
// 위의 if~ else if~ 문이 끝나고 난 뒤 pre에는 특정 데이터를 가진 노드의 중위 선행자 노드가 저장되어 있습니다.
if(thtr->right_thread == FALSE){ // 해당 링크가 중위 후행자와 연결되어 있지 않을 때만 실행됩니다.
In_Order_Traverse_Predecessor(thtr->right_child, data);
}
}
}
중복되는 설명은 제외했습니다.
기본적으로 특정 노드의 중위 후행자는 '특정 노드의 오른쪽 서브트리 가장 왼쪽에 있다.'를 기억하시면 됩니다.
void In_Order_Traverse_Successor(Node *thtr, char data){ // 특정 데이터를 가진 노드의 중위 후행자를 찾아 suc에 저장합니다.
if(thtr){
if(thtr->left_thread == FALSE){
In_Order_Traverse_Successor(thtr->left_child, data);
}
if(sig == 0 && thtr->data == data){ // 특정 데이터를 가진 노드를 찾으면 sig를 1로 바꾸고, 중위 후행자를 받을 준비를 합니다.
sig = 1;
}
else if(sig == 1){ // sig가 1일 때 suc에 노드를 저장합니다.
suc = thtr;
sig = 0;
}
if(thtr->right_thread == FALSE){
In_Order_Traverse_Successor(thtr->right_child, data);
}
}
}
void Find_Suc_Pre(Node *thtr, char data){
pre = NULL;
suc = NULL;
sig = 0;
In_Order_Traverse_Predecessor(thtr, data);
sig = 0;
In_Order_Traverse_Successor(thtr, data);
if(pre == 0){ // 트리의 가장 왼쪽 노드와 가장 오른쪽 노드는 각각 pre와 suc이 없습니다.
pre = head; // 이때 각각은 head를 가리켜야합니다.
}
else if(suc == 0){
suc = head;
}
}
트리에 노드를 추가할 때 해당 노드의 링크가 중위 선행자와 후행자를 가리켜야합니다.
해당 함수는 새로 생성되는 노드의 중위 선행자와 후행자를 찾아주는 역할을 합니다.
2-4. 노드 추가
원하는 데이터와 함께 트리에 노드를 추가합니다.
일반적인 이진 트리와 다르게 자식 노드가 없는 노드는 각자의 중위 선행자와 후행자를 링크에 저장해야 합니다.
이때 위의 Find_Suc_Pre 함수를 사용해 새로 추가 될 노드의 중위 선행자, 중위 후행자 노드를 찾아 연결합니다.
void Input_Data(Thtr *tr, char data){
tr->size ++; // 구조체 배열을 사용하기 때문에 size를 하나 증가시켜줍니다.
int n = tr->size;
tr->thtr[n] = Init_Tree(); // 데이터를 새로 저장할 노드에 메모리를 할당해줍니다.
Node *cur = tr->thtr[n]; // 꼭 필요는 없지만 cur로 새로운 노드를 받아줘야 사용하기 편합니다.
if(n == 1){ // 첫번째 노드는 따로 받아줍니다.
cur->data = data;
cur->left_child = head;
cur->left_thread = TRUE;
cur->right_child = head;
cur->right_thread = TRUE;
level++; // 루트 노드가 level = 1 입니다.
head->left_child = cur; // head 노드의 왼쪽 링크는 항상 root 노드를 가리킵니다.
}
else{
Node *tmp = tr->thtr[n/2]; // 항상 i 번째 노드의 부모 노드는 i/2, 자식 노드는 2*i, 2*i+1 입니다.
// n/2는 항상 내림 됩니다. (n/2가 실제로 1.5라면 1로 반환됩니다.)
if(n % 2 == 0){ // n이 홀수일 땐 부모 노드의 왼쪽에 새로운 노드가 저장됩니다.
tmp->left_child = cur;
tmp->left_thread = FALSE;
}
else if(n % 2 != 0){ // n이 짝수일 땐 부모 노드의 오른쪽에 새로운 노드가 저장됩니다.
tmp->right_child = cur;
tmp->right_thread = FALSE;
}
cur->data = data; // 여기서 데이터를 저장해야 Find_Suc_Pre 함수를 사용할 수 있습니다.
Find_Suc_Pre(tr->thtr[1], data);
cur->left_child = pre; // 새로운 노드의 자식 노드는 없기 때문에 링크에 중위 선행자(pre)와 후행자(suc)를 저장해줍니다.
cur->left_thread = TRUE;
cur->right_child = suc;
cur->right_thread = TRUE;
if(n == pow(2, level) - 1){ // 2의 제곱승의 -1 번째 노드가 각 레벨의 마지막 노드입니다.
level++;
}
}
}
2-5. 중위 선행자, 중위 후행자 탐색 (트리 구성 후 가능)
트리의 모든 링크가 연결된 이후 해당 함수를 사용해 원하는 함수의 중위 선행자 또는 중위 후행자를 찾아 반환 받을 수 있습니다.
Node *InPred(Node *tr){ // 이건 InSucc 함수 논리를 활용해서 만들어 봤습니다. 아래 함수를 참고해주세요.
Node *tmp = tr->left_child;
if(!tr->left_thread){
while(!tmp->right_thread){
tmp = tmp->right_child;
}
}
return tmp;
}
Node *InSucc(Node *tr){
Node *tmp = tr->right_child; // 부모의 오른쪽 자식 노드가 왼쪽 자식노드가 없으면 무조건 부모 노드의 중위 후행자 입니다.
// 만약 right_child가 자식 노드가 아니면 right_child는 애초에 tr 노드의 중위 후행자 입니다.
if(!tr->right_thread){ // 오른쪽 노드가 자식 노드일 때 참입니다.
while(!tmp->left_thread){ // 오른쪽 자식 노드의 왼쪽 자식 노드가 있을 때 참입니다.
tmp = tmp->left_child; // tr의 오른쪽 자식 노드의 왼쪽 자식 노드의 왼쪽 자식 노드의 왼쪽 자식 노드의 ,,,,,,,,
}
} // tr 노드의 오른쪽 서브트리의 가장 왼쪽 노드가 tmp에 저장됩니다.
return tmp;
}
2-6. 트리 출력
트리의 모든 노드를 중위 순회 하며 출력합니다.
이때 시작 노드를 head 노드로 할 때 트리에 저장된 모든 데이터를 출력할 수 있습니다.
void TinOrder(Node *tr){
Node *tmp = tr;
for(;;){
tmp = InSucc(tmp);
if(tmp == tr)
break;
printf("%3c", tmp->data);
}
printf("\n");
}
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
/*--------구조체 선언--------*/
typedef struct NODE{
char data;
struct NODE *left_child;
struct NODE *right_child;
int left_thread;
int right_thread;
} Node;
typedef struct THTR{
Node *thtr[100];
int size;
} Thtr;
/*------------------------*/
/*--------변수 선언--------*/
Node *head;
Node *pre;
Node *suc;
int sig = 0;
int level = 1;
/*-----------------------*/
/*--------함수 선언--------*/
Node *Init_Tree(void);
void In_Order_Traverse_Predecessor(Node *thtr, char data);
void In_Order_Traverse_Successor(Node *thtr, char data);
void Find_Suc_Pre(Node *thtr, char data);
void Input_Data(Thtr *tr, char data);
Node *InPred(Node *tr);
Node *InSucc(Node *tr);
void TinOrder(Node *tr);
/*-----------------------*/
int main(void){
head = Init_Tree();
Thtr tr;
tr.size = 0;
head->left_thread = FALSE;
head->right_child = head;
head->right_thread = FALSE;
Input_Data(&tr, 'a');
printf("tr.thtr[1]->data = %c\n", tr.thtr[1]->data);
Input_Data(&tr, 'b');
printf("tr.thtr[2]->data = %c\n", tr.thtr[2]->data);
Input_Data(&tr, 'c');
printf("tr.thtr[3]->data = %c\n", tr.thtr[3]->data);
Input_Data(&tr, 'd');
printf("tr.thtr[4]->data = %c\n", tr.thtr[4]->data);
Input_Data(&tr, 'e');
printf("tr.thtr[5]->data = %c\n", tr.thtr[5]->data);
printf("\n\n");
// Find_Suc_Pre(tr.thtr[1], 'e');
//
// printf("pre[5]->data = %c\n", pre->data);
// printf("suc[5]->data = %c\n", suc->data);
suc = InSucc(tr.thtr[2]);
pre = InPred(tr.thtr[2]);
printf("InSucc: suc = %c\n", suc->data);
printf("InPred: pre = %c\n", pre->data);
Find_Suc_Pre(tr.thtr[1], 'b');
printf("Find_Suc_Pre: suc = %c\n", suc->data);
printf("Find_Suc_Pre: pre = %c\n", pre->data);
TinOrder(head);
// suc = InSucc(head);
// 아무것도 없는 애들은 NULL
// tr.thtr[1] = Init_Tree();
//
// if(tr.thtr[1] == NULL){
// puts("aa");
// }
// char compare = 'b';
//
// tr.thtr[1]->data = 'a';
//
// if(tr.thtr[1]->data == compare){
// puts("a");
// }
//
return 0;
}
Node *Init_Tree(void){
Node *tr = (Node *)malloc(sizeof(Node));
tr->data = 0;
tr->left_child = NULL;
tr->right_child = NULL;
tr->left_thread = TRUE;
tr->right_thread = TRUE;
return tr;
}
void In_Order_Traverse_Predecessor(Node *thtr, char data){
if(thtr){
if(thtr->left_thread == FALSE){
In_Order_Traverse_Predecessor(thtr->left_child, data);
}
if(sig == 0 && thtr->data != data){
pre = thtr;
// printf("pre = %c\n", pre->data);
}
else if(sig == 0 && thtr->data == data){
sig = 1;
}
if(thtr->right_thread == FALSE){
In_Order_Traverse_Predecessor(thtr->right_child, data);
}
}
}
void In_Order_Traverse_Successor(Node *thtr, char data){
if(thtr){
if(thtr->left_thread == FALSE){
In_Order_Traverse_Successor(thtr->left_child, data);
}
if(sig == 0 && thtr->data == data){
// printf("thtr = %c\n", thtr->data);
sig = 1;
}
else if(sig == 1){
suc = thtr;
// printf("suc = %c\n", suc->data);
sig = 0;
}
if(thtr->right_thread == FALSE){
In_Order_Traverse_Successor(thtr->right_child, data);
}
}
}
void Find_Suc_Pre(Node *thtr, char data){
pre = NULL;
suc = NULL;
sig = 0;
In_Order_Traverse_Predecessor(thtr, data);
sig = 0;
In_Order_Traverse_Successor(thtr, data);
if(pre == 0){
pre = head;
}
else if(suc == 0){
suc = head;
}
}
void Input_Data(Thtr *tr, char data){
tr->size ++;
int n = tr->size;
tr->thtr[n] = Init_Tree();
Node *cur = tr->thtr[n];
if(n == 1){
cur->data = data;
cur->left_child = head;
cur->left_thread = TRUE;
cur->right_child = head;
cur->right_thread = TRUE;
level++;
head->left_child = cur;
}
else{
Node *tmp = tr->thtr[n/2];
if(n % 2 == 0){
tmp->left_child = cur;
tmp->left_thread = FALSE;
}
else if(n % 2 != 0){
tmp->right_child = cur;
tmp->right_thread = FALSE;
}
cur->data = data;
printf("\ncheck[%d]: %c\n", n, cur->data);
Find_Suc_Pre(tr->thtr[1], data);
cur->left_child = pre;
cur->left_thread = TRUE;
cur->right_child = suc;
cur->right_thread = TRUE;
if(n == pow(2, level) - 1){
level++;
}
}
}
Node *InPred(Node *tr){
Node *tmp = tr->left_child;
if(!tr->left_thread){
while(!tmp->right_thread){ // 자식이 있으면 조건문이 참이다.
tmp = tmp->right_child; // 현 노드의 오른쪽 서브 트리의 가장 왼쪽 노드가 successor 이다.
}
}
return tmp;
}
Node *InSucc(Node *tr){
Node *tmp = tr->right_child;
if(!tr->right_thread){
while(!tmp->left_thread){
tmp = tmp->left_child; // 현 노드의 오른쪽 서브 트리의 가장 왼쪽 노드가 successor 이다.
}
}
return tmp;
}
void TinOrder(Node *tr){
puts("\nPrinting starts.");
Node *tmp = tr;
for(;;){
tmp = InSucc(tmp);
if(tmp == tr)
break;
printf("%3c", tmp->data);
}
printf("\n");
puts("Printing starts.\n");
}
3-2. 출력 결과

Input_Data 함수를 사용하여 입력한 데이터가 적절한 위치에 저장이 되었습니다.

InSucc, InPred 함수를 사용하여 'b'가 저장된 노드의 중위 후행자와 선행자를 찾은 결과가
Find_Suc_Pre 함스를 사용하여 동일한 노드의 중위 후행자와 선행자를 찾은 결과와 동일한 것을 볼 수 있습니다.

중위 순회를 사용하여 스레드 노드 전체를 출력한 모습입니다.