아래 내용은 참고 문헌을 정리한 것입니다.
실질적인 예제를 확인하고 싶으신 분들은 모델예측제어 두번째 게시물 (아래 링크)을 참조해주세요.
모델예측제어는 공정 모델을 이용해 미래 출력치를 예측하고 이를 최적화하여 얻어진 제어 입력을 사용하는 제어 기법이다.
유한구간 개 루프 최적제어 입력을 폐 루프 제어 형태로 구현하는 기법으로 볼 수도 있다.
모델예측제어의 기본 개념은 Kalman에 의해 상태공간제어 기법이 소개되고, 이에 기반한 최적제어가 활발히 연구되던 1960년대 초에 이미 성립되어 있었다. (Propoi, 1963; Dreyfus, 1965)
실제로 다양한 형태의 한정 조건들을 미래 출력치를 최적화하는 유한 구간 최적제어 문제에 넣음으로써 이들을 모델예측제어 틀 안에서 쉽게 다룰 수 있다.
안전, 환경 규제 등으로 공정 출력들이 정해진 범위 안에 있어야한 한다. 이러한 한정 조건들이 존재하지 않는 경우 이를 효과적으로 제어할 수 있는 다양한 형태의 선형제어 기법들이 존재하지만, 이들은 한정 조건 조노재하에서는 그 효과를 장담할 수 없게 된다. 따라서 모델예측제어가 한저어 조건들을 효과적으로 다룰 수 있는 점은 실제 공정에서 큰 장점이다.
1. 연속공정의 모델예측제어
1) 모델예측 제어의 기본 개념과 안전성
x(k +1) = Ax(k) + Bu(k)
y(k) = Cx(k).
주어진 시간에 공정의 상태 x(k)가 주어지면
이로부터 미래 제어 입력 u(k + j | k)를 이용하여
미래의 상태 x(k + j | k)를 예측할 수 있다.
현재 공정의 상태 => 미래 제어 입력 => 미래의 상태
모델예측제어는 유한한 미래 예측 구간을 설정하고, 그 구간 내에서 u(k + j | k)를 최적화하고
이중 u(k | k)를 다음 시간의 제어 입력 u(k)로 사용하는 기법이다.
예상? --> j = 0 ~ n (설정된 미래 예측 구간)
u(k + j | k)를 최적화
u(k | k + 0)을 뽑아서
다음 제어 입력 u(k)로 사용
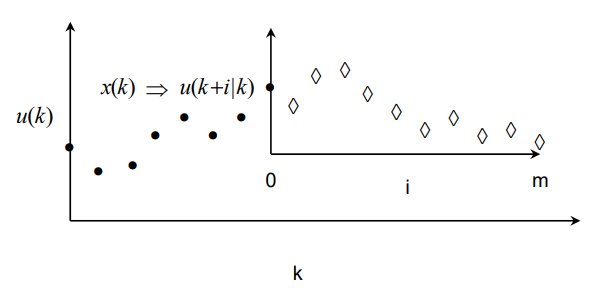
실제로 예측구간에서 u(k + j | k)의 최적화는 대부분 유한구간 개 루프 최적제어 문제이다.
따라서, 일반적으로 개 루프 제어 입력이 얻어진다.
하지만, 실제 제어는 무한 구간에서 폐 루프 제어를 해야한다.
결국, 모델예측제어는 유한구간 개 루프 최적제어 입력을 무한 구간에서 폐 루프 제어로 구현하는 방법이라고 볼 수 있다.
예측구간에서 u(k + j | k)의 최적화에 가장 많이 쓰이는 것은 유한 구간 2차 최적제어이다.
(이때 QP sovler를 사용한다.)
이 경우 매 측정 시간마다 다음의 모델예측제어 문제를 풀어야 한다.
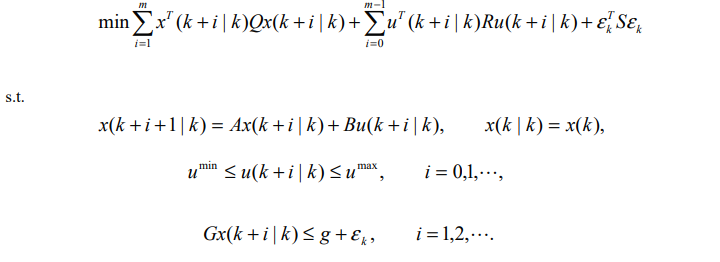
하지만, 이러한 표준 선형 2차 최적제어 문제에 기반한 초기 모델예측제어는 안전성이 명확치 않았다.
실제로 위의 모델예측제어는 일반적으로 폐루프 시스템의 안전성을 보장하지 못 한다. (Bitmead et. al. 1990)
폐 루프 시스템의 안전성을 보장할 수 있는 첫번째 모델예측제어 기법은 1970년대 말에 성립되었다.
이는 표준 선형 2차 최적제어 문제에 최종 상태가 0이 되도록 한정 조건 x(k + m) = 0을 삽입하는 것이다.
(j = 1 ~ m)
이러한 최종 상태의 한정 조건 존재하에서 폐 루프 시스템의 점근 안정성이 보장됨이 증명되었다.
이후 비선형인 경우로도 확장되었다.
90년대 초반에는 안전성을 보장하는 새로운 모델예측제어 기법이 소개되었다.
새로운 기법은 최종 상태 한정 조건 대신 다음과 같은 무한 구간 목적함수를 채택하였다.
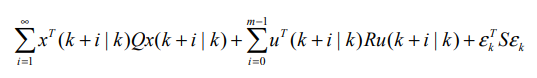
이 방법은 기존의 최종 상태 한정 조건을 이용한 모델예측제어기법을 포괄하는 진일보한 방법이다.
Rawlings와 Muske는 이 방법이 점근성을 보장함을 증명했다.
Zheng과 Morari는 이 방법이 안전한 공정에 대해 출력 되먹임의 경우에도 점근성을 보장함을 증명했다.
현재 세계적으로 가장 널리 쓰이는 모델예측제어 제품으로는 70 년대 말 모델예측제어의 유 용성을 발견해낸 Cutler 그룹이 속한 DMC 사가 만든 DMC 와 Richalet 그룹이 속해 있는 Andersa 에서 만든 IDCOM, HIECON 등이 있다.
이외에 널리 쓰이는 것들로는 Setpoint 사의 SMPC, Honeywell Profimatics 의 RMPCT 그리고 Treiber Controls 의 OPC 를 들 수 있다. 현재 ASPEN 사는 DMC 사와 Setpoint 사를 인수하여 DMC 와 SMPC 를 접목을 시도하고 있는 중이 다.
2. 예측제어의 마이크로콘트롤러 구현을 위한 QP 해법과 그 적용방법
예측 제어는 산업계 및 학계에서 많은 관심을 받아왔고, 특히 응답이 비교적 느린 공정 시스템의 제어에 적합하다고 알려져 있다.
모델 정보를 이용해 시스템의 미래 출력을 예측하고 예측된 출력에 의해 발생된 비용 함수가 최소가 될 수 있도록 시스템의 제어 입력을 최적화 연산을 통해 계산하는 제어 방식이다.
모델 정보 --> 미래 출력 예측 --> 비용 함수 --> 최적화 (QP sovler) --> 제어 입력 도출
예측 제어는 모델식의 종류에 따라 다양함
=> ARMA를 가정하는 GPC
=> 스텝 응답 모델을 사용하는 DMC (Dynamic Matrix Control)
=> 상태 공간 모델을 사용하는 MPC (Model Predictive Control)
비용함수를 최소로 만든다는 최적제어의 개념과
입력과 출력에 나타나는 제약조건을 조직적으로 고려할 수 있는 장점을 가진다.
모델예측제어의 장점
1) 최적제어: 비용함수를 최소로 만든다.
2) 제약조건: 입력과 출력에 나타나는 제약조건을 조직적으로 고려한다.
예측제어의 해를 구하는 문제는 선형행렬부등식 (LMI) 문제로 귀결되는 일부를 제외하고
대부분 QP 문제로 귀결된다.
C-code로 QP solver를 적요한 MPC의 구현 연구가 적은 이유는 다음과 같다
1) MCU에 탑재할 만큼 간결한 C-code 알고리즘을 구하기 힘듦
2) QP 문제의 풀이에 소요되는 시간이 길어 실시간 시스템에 적용 가능성이 떨어진다고 판단
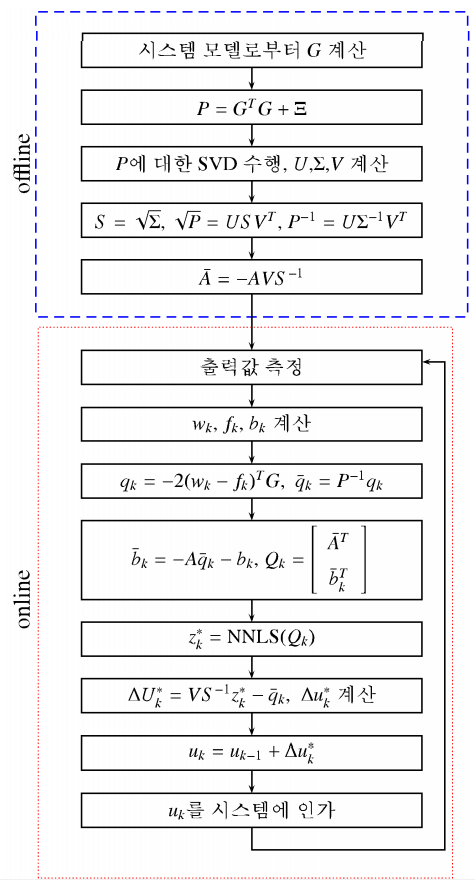
상태 공간 모델을 사용하는 경우 실시간 QP를 푸는 대신 오프라인 계슨을 통해 예측제어의 해를 모든 상태변수에 대해 영역별로 미리 구해 놓고 실시간 연수에선 상태변수가 속한 영역을 검사한 후 그 영역에서의 제어 법칙을 적용하는 방법이 제안됨.
=> 이거 뭐라 그러더라... 무슨 테이블 만들고 테이블 범위에 따라 미리 계산된 결과를 적용함.
실시간 제어하는데 MPC를 사용할 수 있도록 하는 방법을 제안한다.
이를 위해 특이값 분해를 이용하여 QP 문제의 해를 제안하고, 예측제어를 실시간 적용하는데 제안된 QP 문제의 해를 활용할 수 있도록 계산 속도를 향상하는 방법을 제안한다.
특이값 분해를 이용한 QP 문제의 해를 제시
->
예측제어 문제가 QP 문제로 설정됨을 기술
->
제안된 QP의 해를 예측제어 알고리즘에 적용할 때 계산속도를 향상하는 방법을 제안
->
제안된 방법을 적용한 예측 제어 알고리즘을 MCU 상에서 구동함 (실시간 계산 성능 확보 가능 예시)
2-1. 특이값 분해를 이용한 QP 문제의 해
QP 문제는 다음과 같이 기술된다.
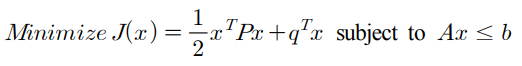
P >= 0 이면, QP 문제는 covex -> 전역해가 존재: global solution
P > 0 이면 -> 유일해가 존재: unique solution
예측제어에서 제어입력 계산 문제는 P > 0인 QP 문제로 귀결된다.
P > 0인 경우의 QP 문제에 대한 해는 다음과 같이 유도된다.
다음과 같은 LSI (Least Squares with Inequality) 문제를 생각하자.
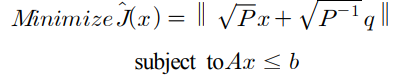
비용한수 J_hat(x)에 대해 다음 식이 성립한다. (윗 식을 제곱하면,,,)
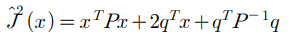
따라서 QP 문제의 비용함수 J(x)와 LSI 문제의 비용함수 J_hat(x)는 다음의 관계가 성립한다.
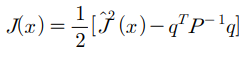
J_hat(x) >= 0이고 (norm이니까? 저 기호의 의미) J는 J_hat의 단조 증가함수이므로 결국 J_hat이 최소일 때 J도 최소값을 가진다.
즉 원래의 QP 문제가 LSI 문제로 등가변형됨을 알 수 있다.
C. L. Lawson and R. J. Hanson, Solving Least Squares Problems, Prentice-Hall, Englewood Cliffs, New Jersey, 1974
위 논문에서 LSI 문제는 LDP (Least Distance Programming)으로 등가 변형 후 NNLS (Nonnegative Least Squares) 문제로 최종적으로 변형할 수 있는 것이 증명되었다.
QP -> LSI -> LDP -> NNLS
이를 이용한 P > 0인 경우의 QP 문제에 대한 풀이법은 다음과 같다.

P > 0이므로 S는 항상 역행렬이 존재한다. (특이값 행렬, 역행렬 존재 조건 확인)
U는 단위 직교행렬이므로 다음이 성립한다.
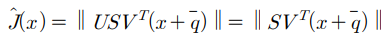
여기서 아래와 같이 가정하면,
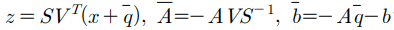
최적화 문제는 다음과 같은 LDP (Least Distance Programming) 문제로 변형된다.
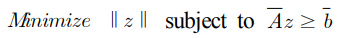
LDP 문제의 해를 z*라고 했을 때 다음과 같은 NNLS 문제를 풀어 그 해를 통해 구할 수 있다. (윗 논문 참고)
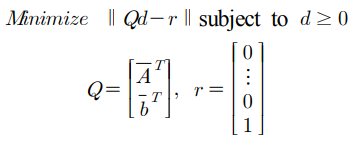
NNLS 문제의 해를 d*라고 하면 LDP 문제의 해 z*는 다음과 같다.
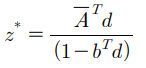
z*로부터 원래의 QP 문제의 해 x*를 다음과 같이 구할 수 있다.
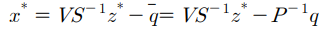
P, q, A, b가 주어졌을 때 QP의 해를 얻기 위해 필요한 계산들은 다음과 같다.
1) 행렬간의 곱, 행렬과 벡터의 곱, 벡터의 덧셈 및 뺄셈
2) P^(1/2)에 대한 특이값 분해
3) P^(-1)를 계산하기 위한 역행렬 계산
4) NNLS 풀이
2), 3), 4)에 대한 계산은 C-code로 구현하기에 비교적 길다.
2), 3)은 행렬의 특이값 분해를 통해 계산 가능
4)는 위 논문에서 제시된 알고리즘을 통해 계산 가능
2)와 3)이 특이값 분해를 통해 계산 가능한 것을 살펴보자.
P가 다음과 같이 특이값 분해가 된다고 가정한다.

P>0이므로, sigma > 0이고, U = V가 성립한다.
U는 단위 직교 행렬이므로, 다음이 성립한다.
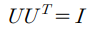
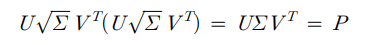
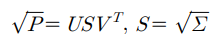
시그마는 대각행렬이므로 S도 대각행렬이고,
S의 주대각선 성분은 시그마의 주대각성 성분에 대한 제곱근 값을 갖는다. => 2번
=> 계산이 쉽다.
P의 역행렬을 계산하기 위해 LU 분해에 이은 back substitution 방법이나 Cramer rule과 같은 역행렬 계산 방법을 사용할 수 있다.
하지만, 여기선 P의 특이값 분해를 계속 사용하여 계산할 수 있다.
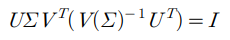
위와 같은 식이 성립하므로, 다음이 성립하는 것을 알 수 있다.
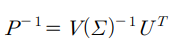
시그마의 역행렬 역시 주대각선 성분에 대한 역수만 계산하면 되므로 쉽게 계산이 가능하다. => 3번
2-2. 예측제어 문제의 QP 문제로의 설정
변수에 사용된 아래 첨자는 시점을 나타내는 것으로 가정한다.
-> 현재 시점 = k
입력은 u라고 한다. u_k+j는 현재 시점으로부터 j 스텝 이후의 입력을 의미한다.
예측제어에서는 매 스텝마다 다음과 같이 제약조건을 만족하면서 주어진 비용함수를 최소화하는 제어량을 계산한다.
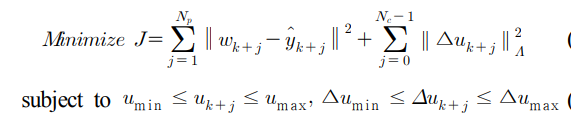

즉, 입력에 대한 최대, 최소값과 입력 증분에 대한 최대 최소값을 정의한 후에
기준 입력과 예측 출력 사이의 오차와 입력 증분을 최소화 할 수 있는 제어 증분량을 계산한다.
예측제어는 매 스텝마다 k+Nc-1까지 제어증분량을 계산한다.
(minimize에서 k+j를 보면 옆에 j가 0 ~ Nc-1까지 변한다.)
하지만, 여기서 사용되는 것은 k 시점에서의 제어 증분량이고 실제 시스템에서 사용되는 제어입력은 다음과 같다.
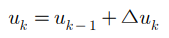
현재로부터 Np 스텝 이후까지의 예측 출력을 행렬과 벡터를 이용하여 나타내면 다음과 같이 나타낼 수 있다.
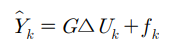
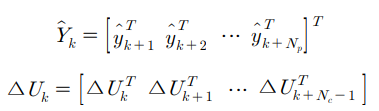
G는 시스템의 모델정보를 이용하여 계산한 예측행렬이고, fk는 free response로써 과거의 data가 미래의 출력에 기여하는 양을 나타낸다.
G는 시간에 대해 불변하기 때문에 아래 첨자가 없다.
G와 fk는 DMC. GPC, MPC 등 예측제어의 종류에 따라 각각의 계산 방식이 존재한다.
미래의 기준 입력 벡터를 아래와 같이 정의한다. (이부분 확인)
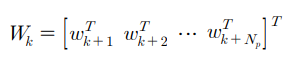
예측제어에서 최소화하고자 하는 비용함수는 Uk의 변화량에 대한 함수가 되어 다음과 같이 나타낼 수 있다.
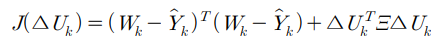
여기서
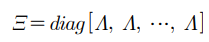
비용함수를 풀어서 Uk의 변화량에 대한 2차형으로 정리하면 다음과 같다.
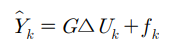
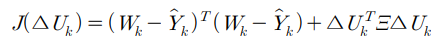
위 두식을 사용한다.
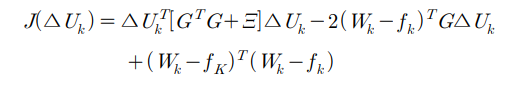
기준 입력을 어떻게 구하지..?
시스템이 갖는 입력 제약조건을 다시 나타내면 다음과 같다.
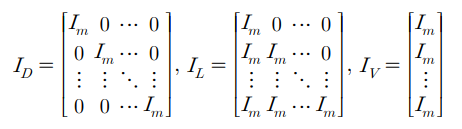
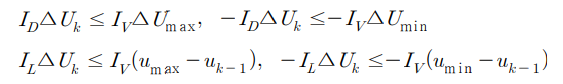
m은 입력의 차원이고, 위 행렬운 예측구간 및 제어구간의 길이에 따라 적절한 차원을 가진다.
이것을 Ax <= b 형태로 나타내면 다음과 같다.
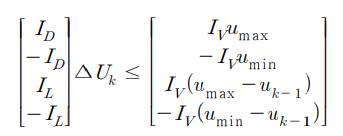
비용함수 (아래 식)에서 마지막 항은 Uk의 변화량 함수가 아니므로 최적화와는 무관하다.
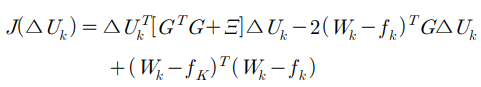
따라서 제약조건 (아래 식)을 만족 시키면서 비용함수 (위 식)을 최소화 시키는 Uk의 변화량은
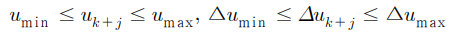
아래 QP 문제의 해가 된다.
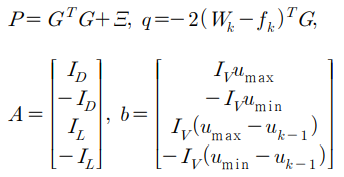
P에 Uk 증분량을 곱하면 비용함수가 됨
예측제어를 구하기 위해 풀어야 하는 QP 문제는 P, q, A, b 중에서 q와 b만이 매 스텝마다 값이 변하게된다.
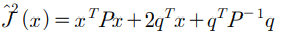
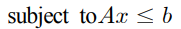
이러한 특징을 활용한 알고리즘을 통해 예측 제어를 비교적 빠른 시스템에도 실시간 적용할 수 있을 정도의 계산 성능을 얻는 방법을 제안한다.

'Study > Control Theory' 카테고리의 다른 글
| 조향 제어/모터 제어 (0) | 2020.04.10 |
|---|---|
| [제어이론] 모델 예측 제어 (MPC: Model Predictive Control) (3) (0) | 2020.04.10 |
| [제어이론] 모델 예측 제어 (MPC: Model Predictive Control) (2) (0) | 2020.04.10 |